【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值M.
上的最大值M.
参考答案:
【答案】(Ⅰ)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,ih根据导函数符号确定单调区间,(2)先求导数,再求导函数零点,讨论零点![]() 与k大小,根据导函数符号确定最大值取法:最大值为
与k大小,根据导函数符号确定最大值取法:最大值为![]() 或
或![]() .最后利用导数比较
.最后利用导数比较![]() 大小,进而确定最大值M.
大小,进而确定最大值M.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
由![]() ,解得
,解得![]() .
.
由![]() ,解得
,解得![]() .
.
由![]() ,解得
,解得![]() .
.
∴函数![]() 的单调增区间为
的单调增区间为![]() ,
,
单调减区间为![]()
(2)因为![]() ,∴
,∴![]() .
.
令![]() ,解得
,解得![]()
因为![]() ,∴
,∴![]() ,∴
,∴![]() .
.
设![]() ,
, ![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,即
,即![]() .
.
∴![]() ,
, ![]() 随x的变化情况如下表:
随x的变化情况如下表:
|
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
∴函数![]() 在[0,k]上的最大值为
在[0,k]上的最大值为![]() 或
或![]() .
.
![]() ,
,
![]()
![]()
因为![]() ,∴
,∴![]() .
.
令![]() ,则
,则![]() .
.
对任意的![]() ,
, ![]() 的图象恒在
的图象恒在![]() 的图象的下方,
的图象的下方,
∴![]() ,即
,即![]()
∴函数![]() 在
在![]() 上为减函数,
上为减函数,
故![]() ,
,
∴![]() ,即
,即![]() .
.
∴函数![]() 在
在![]() 的最大值
的最大值![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中, PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,
 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.(Ⅰ)求证:AD⊥CG;
(Ⅱ)求平面BCP与平面DCP的夹角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
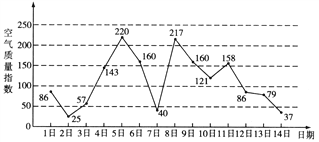
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率
 ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A, 两点
两点 .
.(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,
 ,过P、
,过P、 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若 ,求圆Q的标准方程.
,求圆Q的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆
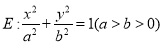 的离心率为
的离心率为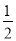 ,圆
,圆 与
与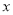 轴交于点
轴交于点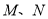 ,
, 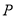 为椭圆
为椭圆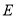 上的动点,
上的动点,  ,
, 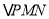 面积最大值为
面积最大值为 .
.(I)求圆
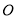 与椭圆
与椭圆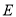 的方程;
的方程;(II)圆
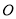 的切线
的切线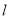 交椭圆于点
交椭圆于点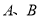 ,求
,求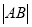 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
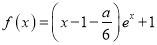 ,其中
,其中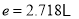 为自然对数的底数,常数
为自然对数的底数,常数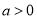 .
.(1)求函数
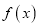 在区间
在区间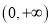 上的零点个数;
上的零点个数;(2)函数
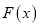 的导数
的导数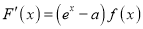 ,是否存在无数个
,是否存在无数个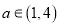 ,使得
,使得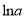 为函数
为函数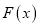 的极大值点?说明理由.
的极大值点?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
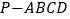 ,底面
,底面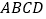 为菱形,
为菱形,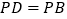 ,
,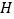 为
为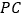 上的点,过
上的点,过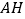 的平面分别交
的平面分别交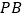 ,
, 于点
于点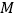 ,
,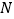 ,且
,且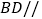 平面
平面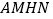 .
.(1)证明:
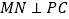 ;
;(2)当
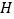 为
为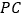 的中点,
的中点,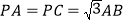 ,
,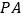 与平面
与平面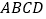 所成的角为
所成的角为 ,求二面角
,求二面角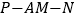 的余弦值.
的余弦值.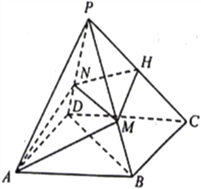
相关试题

