【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
参考答案:
【答案】(1)极小值为![]() ;(2)
;(2)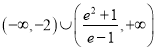
【解析】试题分析:(1)求出函数的导数,计算![]() 的值,求出
的值,求出![]() ,从而求出
,从而求出![]() 的单调区间,求出函数的极值即可;(2)令
的单调区间,求出函数的极值即可;(2)令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,从而求出
的最小值,从而求出![]() 的范围即可.
的范围即可.
试题解析:(1)![]() (
(![]() ),因为曲线
),因为曲线![]() 在点(1,f(1))处的切线与直线
在点(1,f(1))处的切线与直线![]() 垂直,所以
垂直,所以![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() , ∴当
, ∴当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值
,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值![]() ,∴f(x)极小值为ln2.
,∴f(x)极小值为ln2.
(2)令![]() ,则
,则![]() ,欲使在区间上
,欲使在区间上![]() 上存在
上存在![]() ,使得
,使得![]() ,只需在区间
,只需在区间![]() 上
上![]() 的最小值小于零.令
的最小值小于零.令![]() 得,
得, ![]() 或
或![]() .当
.当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,此时
,此时![]() 不成立.综上所述,实数m的取值范围为
不成立.综上所述,实数m的取值范围为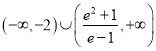
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为
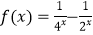 .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价定为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.
(1)设一次订购量为x张,课桌的实际出厂单价为P元,求P关于x的函数关系式P(x);
(2)当一次订购量x为多少时,该家具厂这次销售课桌所获得的利润f(x)最大?其最大利润是多少元?(家具厂售出一张课桌的利润=实际出厂单价﹣成本). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ 或x>﹣
或x>﹣  }
}
C.{x|﹣ <x<﹣
<x<﹣  }
}
D.{x|﹣3<x<﹣2} -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}是等差数列,若
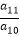 <﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
<﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
A.11
B.17
C.19
D.21 -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形
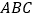 中,若
中,若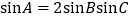 ,则
,则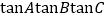 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市五一假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物全额9折优惠;超过300元的其中300 元仍按9折优惠,超过部分按8折优惠.
(1)写出顾客购物全额与应付金额之间的函数关系,并画出流程图,要求输入购物全额,能输出应付金额.
(2)若某顾客的应付金额为282.8元,请求出他的购物全额.
相关试题

