【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() 为椭圆
为椭圆![]() 上的动点,
上的动点, ![]() ,
, ![]() 面积最大值为
面积最大值为![]() .
.
(I)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(II)圆![]() 的切线
的切线![]() 交椭圆于点
交椭圆于点![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .(II)
.(II)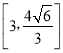
【解析】【试题分析】(1)根据离心率可有![]() ,依题意可知
,依题意可知![]() 为椭圆的焦点,故
为椭圆的焦点,故![]() .当
.当![]() 位于椭圆上顶点时,面积取得最大值,由此列方程可解得
位于椭圆上顶点时,面积取得最大值,由此列方程可解得![]() 的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为
的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为![]() ,利用圆和直线相切求得
,利用圆和直线相切求得![]() 的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线
的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线![]() 的方程为
的方程为![]() ,可直接得到
,可直接得到![]() 的坐标求出弦长.
的坐标求出弦长.
【试题解析】
(1)由题意得![]() ,解得:
,解得: ![]() ①
①
因为![]() ,所以,点
,所以,点![]() 为椭圆的焦点,所以,
为椭圆的焦点,所以, ![]()
设![]() ,则
,则![]() ,所以
,所以![]() ,当
,当![]() 时,
时,
![]() ,代入①解得
,代入①解得![]() ,所以
,所以![]() ,
,
所以,圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
, ![]()
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() ,
,
联立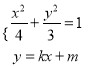 ,消去
,消去![]() 可得
可得![]() ,
,
![]() ,
,
![]()
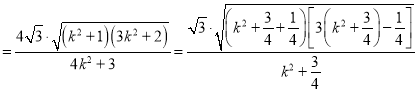
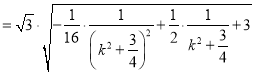
令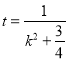 ,则
,则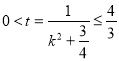 ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]()
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,解得
,解得![]() ,
,
综上, ![]() 的取值范围是
的取值范围是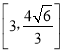 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
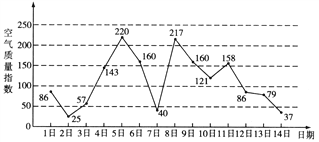
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率
 ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A, 两点
两点 .
.(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,
 ,过P、
,过P、 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若 ,求圆Q的标准方程.
,求圆Q的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
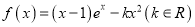 .
.(Ⅰ)当
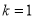 时,求函数
时,求函数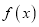 的单调区间;
的单调区间;(Ⅱ)当
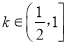 时,求函数
时,求函数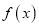 在
在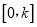 上的最大值M.
上的最大值M. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
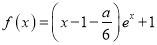 ,其中
,其中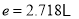 为自然对数的底数,常数
为自然对数的底数,常数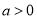 .
.(1)求函数
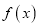 在区间
在区间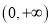 上的零点个数;
上的零点个数;(2)函数
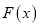 的导数
的导数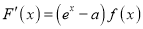 ,是否存在无数个
,是否存在无数个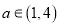 ,使得
,使得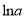 为函数
为函数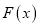 的极大值点?说明理由.
的极大值点?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
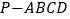 ,底面
,底面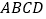 为菱形,
为菱形,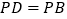 ,
,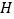 为
为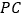 上的点,过
上的点,过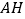 的平面分别交
的平面分别交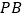 ,
, 于点
于点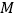 ,
,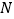 ,且
,且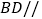 平面
平面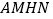 .
.(1)证明:
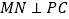 ;
;(2)当
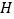 为
为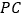 的中点,
的中点,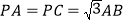 ,
,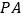 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角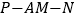 的余弦值.
的余弦值.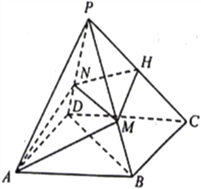
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
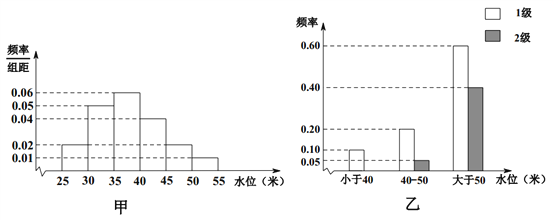
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案
防控等级
费用(单位:万元)
方案一
无措施
0
方案二
防控1级灾害
40
方案三
防控2级灾害
100
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
相关试题

