【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 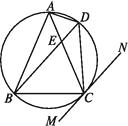
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
参考答案:
【答案】
(1)证明:∵BD∥MN,∴∠CDB=∠DCN.
又∠BAE=∠CDB,
∴∠BAE=∠DCN.
又直线MN是☉O的切线,
∴∠DCN=∠CAD.
∴∠BAE=∠CAD.
又∠ABE=∠ACD,AB=AC,
∴△ABE≌△ACD.
(2)证明:∵∠EBC=∠BCM,∠BCM=∠BDC,
∴∠EBC=∠BDC.
∴CB=CD.
∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,
∴∠BEC=∠EBC+∠ABE=∠ABC.
又AB=AC,
∴∠ABC=∠ECB.
∴∠BEC=∠ECB.
∴BE=BC.
【解析】本题主要考查了弦切角的性质,解决问题的关键是根据弦切角的性质(1)由已知,得∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  点
点 是
是 边的中点,将
边的中点,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,连接
,连接 得到如图
得到如图 所示的几何体.
所示的几何体.
(1)求证;
 平面
平面 ;
;(2)若
 二面角
二面角 的平面角的正切值为
的平面角的正切值为 求二面角
求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
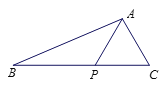
查看答案和解析>>【题目】如图, 在△
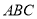 中, 点
中, 点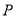 在
在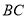 边上,
边上, 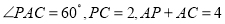 .
.(Ⅰ)求
 ;
;(Ⅱ)若△
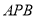 的面积是
的面积是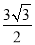 , 求
, 求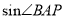 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
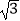 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8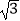 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x+1),g(x)=loga(1﹣x)(a>0且a≠1).
(1)求f(x)+g(x)的定义域;
(2)判断函数f(x)+g(x)的奇偶性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?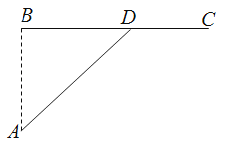
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是
A.命题“对
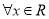 ,都有
,都有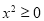 ”的否定为“
”的否定为“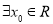 ,使得
,使得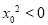 ”
”B.“
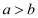 ”是“
”是“ ”的必要不充分条件
”的必要不充分条件C. “若
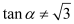 ,则
,则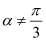 ” 是真命题
” 是真命题D.甲、乙两位学生参与数学模拟考试,设命题
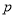 是“甲考试及格”,
是“甲考试及格”,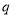 是“乙考试及格”,则命题“至少有一位学生不及格”可表示为
是“乙考试及格”,则命题“至少有一位学生不及格”可表示为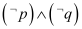
相关试题

