【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2S△ABC=![]()
![]() ·
·![]() .
.
(1)求角B的大小;
(2)若b=2,求a+c的取值范围.
参考答案:
【答案】见解析
【解析】解:(1)由已知得acsin B=![]() accos B,∴tan B=
accos B,∴tan B=![]() ,
,
∵0<B<π,∴B=![]() .
.
(2)法一:由余弦定理得4=a2+c2-2accos ![]() ,即4=(a+c)2-3ac≥(a+c)2-3
,即4=(a+c)2-3ac≥(a+c)2-3![]() 2(当且仅当a=c时取等号),解得0<a+c≤4.
2(当且仅当a=c时取等号),解得0<a+c≤4.
又a+c>b,∴2<a+c≤4,∴a+c的取值范围是(2,4].
法二:由正弦定理得a=![]() sin A,c=
sin A,c=![]() sin C,
sin C,
又A+C=![]() ,∴a+c=
,∴a+c=![]() (sin A+sin C)=
(sin A+sin C)=![]() [sin A+sin(A+B)]=
[sin A+sin(A+B)]=
![]()
![]() =4
=4![]() =4sin
=4sin![]() .
.
∵0<A<![]() ,∴
,∴![]() <A+
<A+![]() <
<![]() ,∴
,∴![]() <sin
<sin![]() ≤1,∴a+c的取值范围是(2,4].
≤1,∴a+c的取值范围是(2,4].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
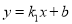 与反比例函数
与反比例函数 的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。⑴ 求
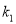 ,
, 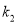 的值;
的值;⑵ 直接写出
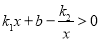 时,
时, 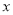 的取值范围。
的取值范围。 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①函数y=
 的定义域为{x|x≥1};
的定义域为{x|x≥1};②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|(x-3)(x+a)<0,a∈R},集合B={x∈Z|x2-3x-4<0}.
(1)若A∩B的子集个数为4,求a的范围;
(2)若a∈Z,当A∩B≠
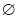 时,求a的最小值,并求当a取最小值时A∪B.
时,求a的最小值,并求当a取最小值时A∪B. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图①,正三角形
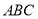 的边长为4,
的边长为4,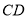 是
是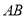 边上的高,
边上的高,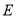 ,
,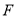 分别是
分别是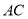 和
和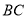 边的中点,现将△
边的中点,现将△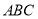 沿
沿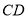 翻折成直二面角
翻折成直二面角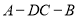 ,如图②.
,如图②.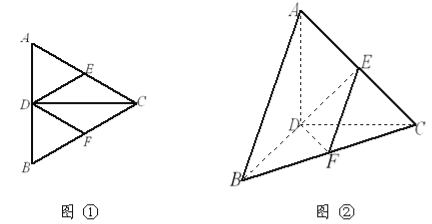
(1)判断直线
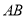 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求棱锥
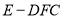 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:
 ,
,  ,
,  ,…
,… 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
相关试题

