【题目】已知如图①,正三角形![]() 的边长为4,
的边长为4,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 边的中点,现将△
边的中点,现将△![]() 沿
沿![]() 翻折成直二面角
翻折成直二面角![]() ,如图②.
,如图②.
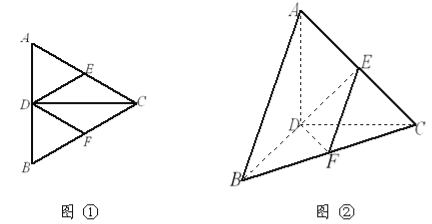
(1)判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)直线![]() 平面
平面![]() ,理由见解析;(2)
,理由见解析;(2)![]() .
.
【解析】
试题分析:(1)利用线面平行证得![]() ,利用线面平行判定定理证得
,利用线面平行判定定理证得![]() 平面
平面![]() ;(2)利用二面角
;(2)利用二面角![]() 是直二面角,得平面
是直二面角,得平面![]() 平面
平面![]() ,利用面面垂直的判定定理证得
,利用面面垂直的判定定理证得![]()
![]() ,然后利用线面垂直的判定定理证得
,然后利用线面垂直的判定定理证得![]() 平面
平面![]() ,从而求得点
,从而求得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求得
,求得![]() ,利用空间几何体的体积公式求得棱锥
,利用空间几何体的体积公式求得棱锥![]() 的体积.
的体积.
试题解析:(1)证明:直线![]() 平面
平面![]() .
.
在△![]() 中,
中,![]() ,
,![]() 为中点,
为中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵二面角![]() 是直二面角,
是直二面角,
∴平面![]() 平面
平面![]() ,
,
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]()
![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
又∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2S△ABC=
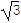
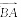 ·
·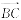 .
.(1)求角B的大小;
(2)若b=2,求a+c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|(x-3)(x+a)<0,a∈R},集合B={x∈Z|x2-3x-4<0}.
(1)若A∩B的子集个数为4,求a的范围;
(2)若a∈Z,当A∩B≠
 时,求a的最小值,并求当a取最小值时A∪B.
时,求a的最小值,并求当a取最小值时A∪B. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:
 ,
,  ,
,  ,…
,… 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
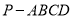 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=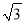 ,
, 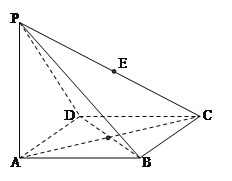
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
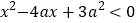 ,其中
,其中 ,命题
,命题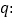 实数
实数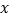 满足
满足|x-3|≤1 .
(1)若
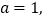 且
且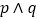 为真,求实数
为真,求实数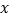 的取值范围;
的取值范围;(2)若
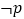 是
是
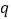 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
相关试题

