【题目】已知△ABC,AB=AC=4,BC=2,点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是 , com∠BDC= .
参考答案:
【答案】![]() ;
;![]()
【解析】解:如图,取BC得中点E,
∵AB=AC=4,BC=2,
∴BE= ![]() BC=1,AE⊥BC,
BC=1,AE⊥BC,
∴AE= ![]() =
= ![]() ,
,
∴S△ABC= ![]() BCAE=
BCAE= ![]() ×2×
×2× ![]() =
= ![]() ,
,
∵BD=2,
∴S△BDC= ![]() S△ABC=
S△ABC= ![]() ,
,
∵BC=BD=2,
∴∠BDC=∠BCD,
∴∠ABE=2∠BDC
在Rt△ABE中,
∵cos∠ABE= ![]() =
= ![]() ,
,
∴cos∠ABE=2cos2∠BDC﹣1= ![]() ,
,
∴cos∠BDC= ![]() ,
,
所以答案是: ![]() ,
, ![]()

【考点精析】通过灵活运用二倍角的余弦公式,掌握二倍角的余弦公式:![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
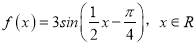 .
.(1)利用“五点法”画出函数
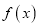 在一个周期
在一个周期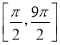 上的简图;
上的简图;(2)先把
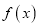 的图象上所有点向左平移
的图象上所有点向左平移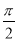 个单位长度,得到
个单位长度,得到 的图象;然后把
的图象;然后把 的图
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到
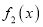 的图象;再把
的图象;再把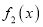 的图象
的图象上所有点的纵坐标缩短到原来的
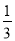 倍(横坐标不变),得到
倍(横坐标不变),得到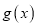 的图象,求
的图象,求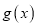 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=60°,AB=3,AC=2.若
 =2
=2  ,
,  =λ
=λ  ﹣
﹣  (λ∈R),且
(λ∈R),且  =﹣4,则λ的值为 .
=﹣4,则λ的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的参数方程是
的参数方程是 为参数
为参数 ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 .
.(1)写出
 的极坐标方程和
的极坐标方程和 的直角坐标方程;
的直角坐标方程;(2)已知点
 、
、 的极坐标分别是
的极坐标分别是 、
、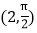 ,直线
,直线 与曲线
与曲线 相交于P、Q两点,射线OP与曲线
相交于P、Q两点,射线OP与曲线 相交于点A,射线OQ与曲线
相交于点A,射线OQ与曲线 相交于点B,求
相交于点B,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将3本相同的小说,2本相同的诗集全部分给4名同学,每名同学至少1本,则不同的分法有( )
A. 24种 B. 28种 C. 32种 D. 36种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x∈[-
 ,
,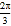 ],
],(1)求函数y=cosx的值域;
(2)求函数y=-3sin2x-4cosx+4的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
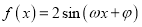 (其中
(其中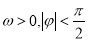 ),若函数
),若函数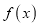 的图象与
的图象与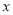 轴的任意两个相邻交点间的距离为
轴的任意两个相邻交点间的距离为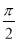 ,且函数
,且函数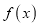 的图象过点
的图象过点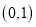 .
.(1)求
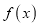 的解析式;
的解析式;(2)求
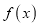 的单调增区间:
的单调增区间:(3)求
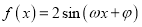 在
在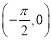 的值域.
的值域.
相关试题

