【题目】有下列命题:①边长为1的正四面体的内切球半径为![]() ;
;
②正方体的内切球、棱切球(正方体的每条棱都与球相切)、外接球的半径之比为1:![]() ;
;
③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为![]() .
.
其中正确命题的序号是______(请填所有正确命题的序号);
参考答案:
【答案】①②③
【解析】
运用正四面体的性质和体积公式,结合等积法可得球的半径,可判断①;
由正方体与内切球、棱切球和外接球的关系,求得半径,可判断②;
求得正方体内切球半径,结合球的截面性质,以及勾股定理和等边三角形的性质,即可判断③.
①边长为1的正四面体的高为h![]() ,
,
可得正四面体的体积为V![]()
![]() h
h![]() ,
,
设内切球的半径为r,由等积法可得V![]() rS
rS![]() r4
r4![]() ,(S为正四面体的全面积)
,(S为正四面体的全面积)
解得r![]() ,故①正确;
,故①正确;
②设边长为1的正方体的内切球、棱切球(正方体的每条棱都与球相切)、外接球的半径
分别为r1,r2,r3,可得2r1=1,2r2![]() ,2r3
,2r3![]() ,
,
即有r1:r2:r3=1:![]() ,故②正确;
,故②正确;
③棱长为1的正方体ABCD﹣A1B1C1D1的内切球的半径为![]() ,
,
设内心为I,可得A1I![]() ,I在截面的射影为等边三角形A1BD的中心O,
,I在截面的射影为等边三角形A1BD的中心O,
可得OI![]() ,
,
由球的截面的性质可得截面圆的半径为![]() ,可得截面圆的面积为
,可得截面圆的面积为![]() ,故③正确.
,故③正确.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过平面直角坐标系中的点P(4-3a,
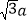 )(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积
)(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积 的最小值为( )
的最小值为( )A.
 B.
B.  C.
C. 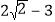 D.
D. 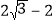
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=3,长方体每条棱所在直线与过点C1的平面α所成的角都相等,则直线AC与平面α所成角的余弦值为( )
A.
 或1 B.
或1 B.  或0 C.
或0 C. 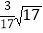 或0 D.
或0 D. 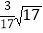 或1
或1 -
科目: 来源: 题型:
查看答案和解析>>【题目】设正项数列
 的前
的前 项和为
项和为 ,且满足:
,且满足: ,
, ,
, .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若正项等比数列
 满足
满足 ,
, ,且
,且 ,数列
,数列 的前
的前 项和为
项和为 ,若对任意
,若对任意 ,均有
,均有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
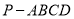 中,底面
中,底面 为正方形,已知
为正方形,已知 ,
,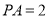 ,
,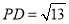 ,
, .
.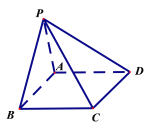
(1)证明:
 面
面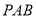 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
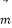 =(2sinx,-1),
=(2sinx,-1),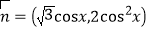 ,函数f(x)=
,函数f(x)=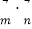 .
.(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
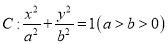 经过点
经过点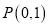 ,离心率
,离心率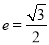 .
.(1)求
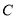 的方程;
的方程;(2)设直线
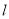 经过点
经过点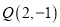 且与
且与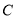 相交于
相交于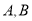 两点(异于点
两点(异于点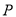 ),记直线
),记直线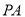 的斜率为
的斜率为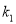 ,直线
,直线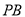 的斜率为
的斜率为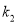 ,证明:
,证明: 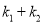 为定值.
为定值.
相关试题

