【题目】设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若正项等比数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意
,若对任意![]() ,均有
,均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)an=2n;(Ⅱ)[![]() ,+∞).
,+∞).
【解析】
(Ⅰ)对递推关系![]() 再递推一步,两式相减,最后结合等差数列的定义进行求解即可;
再递推一步,两式相减,最后结合等差数列的定义进行求解即可;
(Ⅱ)根据等差数列的通项公式结合已知求出等比数列的通项公式,最后利用错位相减法、判断数列的单调性进行求解即可.
(Ⅰ)因为![]() ,所以
,所以![]() (n≥2),
(n≥2),
两式相减得:an+12﹣an2=4an+4,即an+12=(an+2)2(n≥2),
又因为数列{an}的各项均为正数,所以an+1=an+2(n≥2),
又因为a2=4,16=a12+4+4,可得a1=2,
所以当n=1时上式成立,即数列{an}是首项为2、公差为2的等差数列,
所以![]() ;
;
(Ⅱ)由(1)可知b1=a1=2,b3=a4=8,所以正项等比数列![]() 的公比为:
的公比为:![]() ,
,
因此bn=![]() ;cn=
;cn=![]() .
.
![]() ①
①
![]() ②
②
① —②得:
![]()
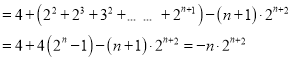
![]()
![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,
恒成立,
所以![]() 恒成立,
恒成立,
设kn=![]() ,则kn+1﹣kn=
,则kn+1﹣kn=![]() ﹣
﹣![]() =
=![]() ,
,
所以当n≤4时kn+1>kn,当n>4时kn+1<kn,
所以![]()
所以当kn的最大值为k5=![]() ,故m≥
,故m≥![]() ,
,
即实数m的取值范围是:[![]() ,+∞).
,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在道路边安装路灯,路面
 宽
宽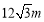 ,灯柱
,灯柱 高14
高14 ,灯杆
,灯杆 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线 与灯杆
与灯杆 垂直,轴线
垂直,轴线 ,灯杆
,灯杆 都在灯柱
都在灯柱 和路面宽线
和路面宽线 确定的平面内.
确定的平面内.
(1)当灯杆
 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线 正好通过路面
正好通过路面 的中线?
的中线?(2)如果灯罩轴线AC正好通过路面
 的中线,此时有一高2.5
的中线,此时有一高2.5  的警示牌直立在
的警示牌直立在 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】过平面直角坐标系中的点P(4-3a,
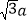 )(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积
)(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积 的最小值为( )
的最小值为( )A.
 B.
B.  C.
C. 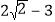 D.
D. 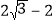
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=3,长方体每条棱所在直线与过点C1的平面α所成的角都相等,则直线AC与平面α所成角的余弦值为( )
A.
 或1 B.
或1 B.  或0 C.
或0 C. 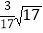 或0 D.
或0 D. 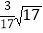 或1
或1 -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①边长为1的正四面体的内切球半径为
 ;
;②正方体的内切球、棱切球(正方体的每条棱都与球相切)、外接球的半径之比为1:
 ;
;③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为
 .
.其中正确命题的序号是______(请填所有正确命题的序号);
-
科目: 来源: 题型:
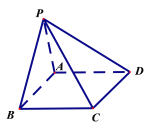
查看答案和解析>>【题目】在四棱锥
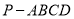 中,底面
中,底面 为正方形,已知
为正方形,已知 ,
,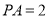 ,
,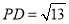 ,
, .
.
(1)证明:
 面
面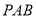 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
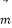 =(2sinx,-1),
=(2sinx,-1),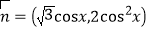 ,函数f(x)=
,函数f(x)=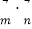 .
.(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
相关试题

