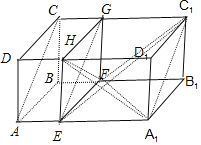
【题目】已知在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=3,长方体每条棱所在直线与过点C1的平面α所成的角都相等,则直线AC与平面α所成角的余弦值为( )
A. ![]() 或1 B.
或1 B. ![]() 或0 C.
或0 C. ![]() 或0 D.
或0 D. ![]() 或1
或1
参考答案:
【答案】A
【解析】
在长方体ABCD-A1B1C1D1中截取一个棱长为2的正方体EFGH-A1B1C1D1,要使长方体每条棱所在直线与过点C1的平面α所成的角都相等,则平面α可视为平面C1FA1及于平面HFA1平行的平面.利用正方体棱的关系,判断平面α所成的角都相等的位置,然后求解直线AC与平面α所成角的余弦值.
如图,在长方体ABCD-A1B1C1D1中截取一个棱长为2的正方体EFGH-A1B1C1D1,
长方体每条棱所在直线与过点C1的平面α所成的角都相等,则平面α可视为平面C1FA1及于平面HFA1平行的平面.
直线AC与平面C1FA1所成角=直线C1A1与平面C1FA1所成角=0,所以余弦值为1,
∵AC∥EG,EC1⊥面FHA1,∴直线AC与平面HFA1所成角的余弦值等于EG与EC1所成角∠GEC1的正弦值,
在直角△EGC1中,![]() ,GC1=2,
,GC1=2,![]() ,
,
∴sin![]() .
.
∴直线AC与平面α所成角的余弦值为1,![]() ,
,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形
 的斜边
的斜边 所在直线方程为
所在直线方程为 ,其中
,其中 点在
点在 点上方,直角顶点
点上方,直角顶点 的坐标为
的坐标为 .
.
(1)求
 边上的高线
边上的高线 所在直线的方程;
所在直线的方程;(2)求等腰直角三角形
 的外接圆的标准方程;
的外接圆的标准方程;(3)分别求两直角边
 ,
, 所在直线的方程.
所在直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在道路边安装路灯,路面
 宽
宽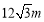 ,灯柱
,灯柱 高14
高14 ,灯杆
,灯杆 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线 与灯杆
与灯杆 垂直,轴线
垂直,轴线 ,灯杆
,灯杆 都在灯柱
都在灯柱 和路面宽线
和路面宽线 确定的平面内.
确定的平面内.
(1)当灯杆
 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线 正好通过路面
正好通过路面 的中线?
的中线?(2)如果灯罩轴线AC正好通过路面
 的中线,此时有一高2.5
的中线,此时有一高2.5  的警示牌直立在
的警示牌直立在 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】过平面直角坐标系中的点P(4-3a,
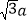 )(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积
)(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积 的最小值为( )
的最小值为( )A.
 B.
B.  C.
C. 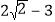 D.
D. 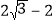
-
科目: 来源: 题型:
查看答案和解析>>【题目】设正项数列
 的前
的前 项和为
项和为 ,且满足:
,且满足: ,
, ,
, .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若正项等比数列
 满足
满足 ,
, ,且
,且 ,数列
,数列 的前
的前 项和为
项和为 ,若对任意
,若对任意 ,均有
,均有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①边长为1的正四面体的内切球半径为
 ;
;②正方体的内切球、棱切球(正方体的每条棱都与球相切)、外接球的半径之比为1:
 ;
;③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为
 .
.其中正确命题的序号是______(请填所有正确命题的序号);
-
科目: 来源: 题型:
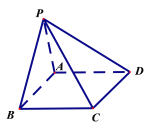
查看答案和解析>>【题目】在四棱锥
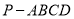 中,底面
中,底面 为正方形,已知
为正方形,已知 ,
,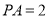 ,
,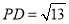 ,
, .
.
(1)证明:
 面
面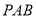 ;
;(2)求二面角
 的大小.
的大小.
相关试题

