【题目】已知椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 经过点
经过点![]() 且与
且与![]() 相交于
相交于![]() 两点(异于点
两点(异于点![]() ),记直线
),记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,证明:
,证明: ![]() 为定值.
为定值.
参考答案:
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)依题意可知![]() ,解方程组可求得椭圆的标准方程.(2)当直线斜率
,解方程组可求得椭圆的标准方程.(2)当直线斜率![]() 斜率不存在时,不符合题意.当斜率存在时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算
斜率不存在时,不符合题意.当斜率存在时,设出直线的方程,联立直线的方程和椭圆的方程,写出韦达定理,计算![]() 的值,化简后结果为
的值,化简后结果为![]() ,由此证明结论成立.
,由此证明结论成立.
【试题解析】
(1)因为椭圆![]() ,经过点
,经过点![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,解得
,解得![]() .
.
故而可得椭圆的标准方程为: ![]() .
.
(2)若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() ,
,
此时直线与椭圆相切,不符合题意.
设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立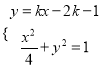 ,得
,得![]() .
.
设![]() ,
, ![]() ,则
,则
![]()
![]()
![]()
![]()
![]()
![]()
所以![]() 为定值,且定值为-1.
为定值,且定值为-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①边长为1的正四面体的内切球半径为
 ;
;②正方体的内切球、棱切球(正方体的每条棱都与球相切)、外接球的半径之比为1:
 ;
;③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为
 .
.其中正确命题的序号是______(请填所有正确命题的序号);
-
科目: 来源: 题型:
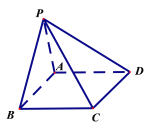
查看答案和解析>>【题目】在四棱锥
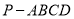 中,底面
中,底面 为正方形,已知
为正方形,已知 ,
,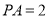 ,
,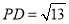 ,
, .
.
(1)证明:
 面
面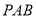 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
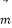 =(2sinx,-1),
=(2sinx,-1),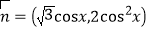 ,函数f(x)=
,函数f(x)=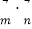 .
.(1)求函数f(x)的对称中心;
(2)设△ABC的内角A,B,C所对的边为a,b,c,且a2=bc,求f(A)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其它两观测点晚4
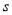 .已知各观测点到该中心的距离是1020
.已知各观测点到该中心的距离是1020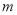 .则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340
.则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340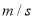 ,相关各点均在同一平面上)
,相关各点均在同一平面上)A. 西偏北
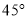 方向,距离
方向,距离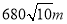 B. 东偏南
B. 东偏南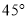 方向,距离
方向,距离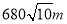
C. 西偏北
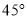 方向,距离
方向,距离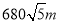 D. 东偏南
D. 东偏南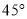 方向,距离
方向,距离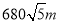
-
科目: 来源: 题型:
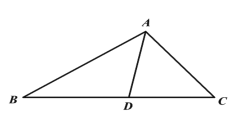
查看答案和解析>>【题目】如图,已知
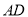 是
是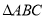 中
中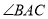 的角平分线,交
的角平分线,交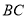 边于点
边于点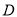 .
.
(1)用正弦定理证明:
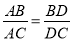 ;
;(2)若
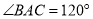 ,
, 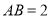 ,
, 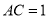 ,求
,求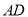 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
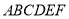 中,平面
中,平面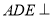 平面
平面 ,四边形
,四边形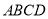 为菱形,且
为菱形,且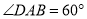 ,
, 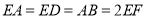 ,
, 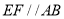 ,
,  为
为 中点.
中点.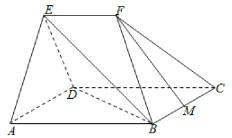
(1)求证:
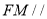 平面
平面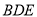 ;
;(2)求二面角
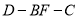 的平面角的正弦值.
的平面角的正弦值.
相关试题

