【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
参考答案:
【答案】(1)![]() ;(2)甲大棚
;(2)甲大棚![]() 万元,乙大棚
万元,乙大棚![]() 万元时,总收益最大, 且最大收益为
万元时,总收益最大, 且最大收益为![]() 万元.
万元.
【解析】试题分析:(1)由题意,把![]() 代入所给函数求出即可;(2)每年两个大棚的总收益为
代入所给函数求出即可;(2)每年两个大棚的总收益为![]() ,确定函数的定义域,利用二次函数图象在闭区间上求最值即可.
,确定函数的定义域,利用二次函数图象在闭区间上求最值即可.
试题解析:(1)因为甲大棚投入![]() 万元,则乙大棚投入
万元,则乙大棚投入![]() 万元,....................1分
万元,....................1分
所以![]() ......................4分
......................4分
(2)![]() ,
,
依题意得![]() ,故
,故![]() ......8分
......8分
令![]() ,
,
则![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() ,
,
所以投入甲大棚![]() 万元,乙大棚
万元,乙大棚![]() 万元时,总收益最大,且最大收益为
万元时,总收益最大,且最大收益为![]() 万元...........12分
万元...........12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
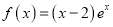 和
和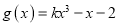 .
.(1)若函数
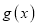 在区间
在区间 不单调,求实数
不单调,求实数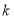 的取值范围;
的取值范围;(2)当
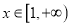 时,不等式
时,不等式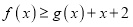 恒成立,求实数
恒成立,求实数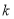 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 上的偶函数,其图象关于点
上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数,则
上是单调函数,则 的值是( )
的值是( )A.
 B.
B.  C.
C.  或
或 D. 无法确定
D. 无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
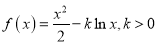 .
.(1)求
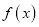 的单调区间和极值;
的单调区间和极值;(2)证明:若
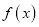 存在零点,则
存在零点,则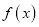 在区间
在区间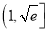 上仅有一个零点.
上仅有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为
 ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为 ,而当年产销量相等。
,而当年产销量相等。(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
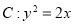 的焦点为
的焦点为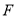 ,平行于
,平行于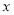 轴的两条直线
轴的两条直线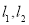 分别交
分别交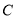 于
于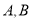 两点,交
两点,交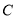 的准线于
的准线于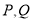 两点 .
两点 .(1)若
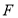 在线段
在线段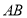 上,
上,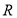 是
是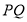 的中点,证明
的中点,证明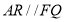 ;
;(2)若
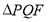 的面积是
的面积是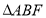 的面积的两倍,求
的面积的两倍,求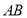 中点的轨迹方程.
中点的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形
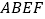 中,
中,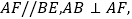 且
且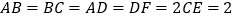 ,沿
,沿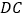 将梯形
将梯形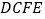 折起,使得平面
折起,使得平面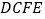 ⊥平面
⊥平面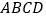
 .
.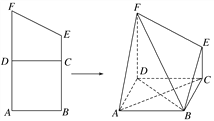
(1)证明:
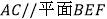 ;
;(2)求三棱锥
 的体积;
的体积;(3)求直线
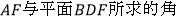 。
。
相关试题

