【题目】已知函数![]() 上的偶函数,其图象关于点
上的偶函数,其图象关于点![]() 对称,且在区间
对称,且在区间![]() 上是单调函数,则
上是单调函数,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. 无法确定
D. 无法确定
参考答案:
【答案】C
【解析】由f(x)是偶函数,得f(﹣x)=f(x),即sin(﹣ωx+![]() )=sin(ωx+
)=sin(ωx+![]() ),
),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且ω>0,所以得cosφ=0.
依题设0<φ<π,所以解得φ=![]() ,
,
由f(x)的图象关于点M对称,得f(![]() ﹣x)=﹣f(
﹣x)=﹣f(![]() +x),
+x),
取x=0,得f(![]() )=sin(
)=sin(![]() +
+![]() )=cos
)=cos![]() ,
,
∴f(![]() )=sin(
)=sin(![]() +
+![]() )=cos
)=cos![]() ,∴cos
,∴cos![]() =0,
=0,
又ω>0,得![]() =
=![]() +kπ,k=1,2,3,
+kπ,k=1,2,3,
∴ω=![]() (2k+1),k=0,1,2,
(2k+1),k=0,1,2,
当k=0时,ω=![]() ,f(x)=sin(x+
,f(x)=sin(x+![]() )在[0,
)在[0,![]() ]上是减函数,满足题意;
]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+![]() )在[0,
)在[0,![]() ]上是减函数;
]上是减函数;
当k=2时,ω=![]() ,f(x)=(
,f(x)=(![]() x+
x+![]() )在[0,
)在[0,![]() ]上不是单调函数;
]上不是单调函数;
所以,综合得ω=![]() 或2.
或2.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( 为参数),曲线
为参数),曲线 (
( 为参数).
为参数).(I)设
 与
与 相交于
相交于 两点,求
两点,求 ;
;(II)若把曲线
 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线 .设点
.设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】记
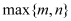 表示
表示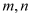 中的最大值,如
中的最大值,如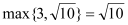 .已知函数
.已知函数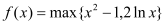 ,
, .
.(1)设
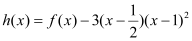 ,求函数
,求函数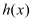 在
在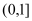 上零点的个数;
上零点的个数; (2)试探究是否存在实数
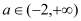 ,使得
,使得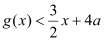 对
对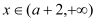 恒成立?若存在,求
恒成立?若存在,求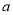 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
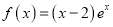 和
和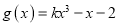 .
.(1)若函数
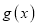 在区间
在区间 不单调,求实数
不单调,求实数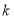 的取值范围;
的取值范围;(2)当
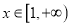 时,不等式
时,不等式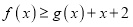 恒成立,求实数
恒成立,求实数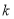 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
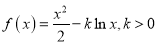 .
.(1)求
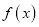 的单调区间和极值;
的单调区间和极值;(2)证明:若
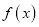 存在零点,则
存在零点,则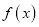 在区间
在区间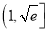 上仅有一个零点.
上仅有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入
 种黄瓜的年收入
种黄瓜的年收入 与投入
与投入 (单位:万元)满足
(单位:万元)满足 .设甲大棚的投入为
.设甲大棚的投入为 (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为 (单位:万元)
(单位:万元)(1)求
 的值;
的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益
 最大?
最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为
 ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为 ,而当年产销量相等。
,而当年产销量相等。(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
相关试题

