【题目】已知函数![]() 和
和![]() .
.
(1)若函数![]() 在区间
在区间![]() 不单调,求实数
不单调,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)依题意![]() ,①当
,①当![]() 时
时![]()
![]()
![]() 所以
所以![]() 在
在![]() 单调递减
单调递减![]() 不满足题意,②当
不满足题意,②当![]() 时,
时,![]() 在
在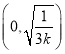 上单调递减,在
上单调递减,在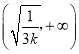 上单调递增
上单调递增![]()
![]()
![]()
![]()
![]() ;(2)由已知得
;(2)由已知得![]() ,令
,令![]() ,再利用导数指数可求得
,再利用导数指数可求得![]()
![]()
![]()
![]() 即
即![]() 的最大值为
的最大值为![]() .
.
试题解析: (1)依题意![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,不满足题意,
单调递减,不满足题意,
②当![]() 时,
时,![]() 在
在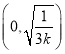 上单调递减,在
上单调递减,在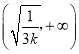 上单调递增,
上单调递增,
因为函数![]() 在区间
在区间![]() 不单调,所以
不单调,所以![]() ,解得
,解得![]() ,
,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .................6分
.................6分
(2)由已知得![]() ,...................7分
,...................7分
令![]() ,则
,则![]() ................10分
................10分
![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,∴
,∴![]() ,即
,即![]() 的最大值为
的最大值为![]() ..................13分
..................13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
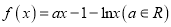 .
.(1)讨论函数
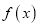 在定义域内的极值点的个数;
在定义域内的极值点的个数;(2)若函数
 在
在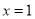 处取得极值,且对
处取得极值,且对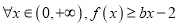 恒成立,求实数
恒成立,求实数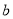 的取值范围;
的取值范围;(3)当
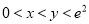 且
且 时,试比较
时,试比较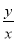 与
与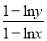 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( 为参数),曲线
为参数),曲线 (
( 为参数).
为参数).(I)设
 与
与 相交于
相交于 两点,求
两点,求 ;
;(II)若把曲线
 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线 .设点
.设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】记
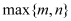 表示
表示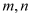 中的最大值,如
中的最大值,如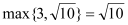 .已知函数
.已知函数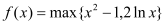 ,
, .
.(1)设
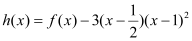 ,求函数
,求函数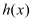 在
在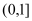 上零点的个数;
上零点的个数; (2)试探究是否存在实数
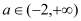 ,使得
,使得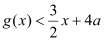 对
对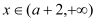 恒成立?若存在,求
恒成立?若存在,求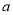 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 上的偶函数,其图象关于点
上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数,则
上是单调函数,则 的值是( )
的值是( )A.
 B.
B.  C.
C.  或
或 D. 无法确定
D. 无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
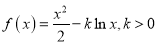 .
.(1)求
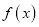 的单调区间和极值;
的单调区间和极值;(2)证明:若
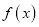 存在零点,则
存在零点,则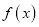 在区间
在区间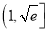 上仅有一个零点.
上仅有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入
 种黄瓜的年收入
种黄瓜的年收入 与投入
与投入 (单位:万元)满足
(单位:万元)满足 .设甲大棚的投入为
.设甲大棚的投入为 (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为 (单位:万元)
(单位:万元)(1)求
 的值;
的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益
 最大?
最大?
相关试题

