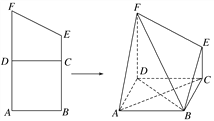
【题目】如图,梯形![]() 中,
中,![]() 且
且![]() ,沿
,沿![]() 将梯形
将梯形![]() 折起,使得平面
折起,使得平面![]() ⊥平面
⊥平面![]()
![]() .
.
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)求直线![]() 。
。
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)取BF中点为M,AC与BD交点为O,连结MO,ME,由已知结合三角形中位线定理可得四边形OCEM为平行四边形,然后利用线面平行的判定得答案;
(2)由线面垂直的性质定理可得BC⊥平面DEF,然后把三棱锥D-BEF的体积转化为三棱锥B-DEF的体积求解.
(3)分析条件得![]() ,连结
,连结![]() ,
,![]() ,由
,由![]() 求解即可.
求解即可.
试题解析:
(1)证明 如图,取BF的中点![]() ,设
,设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() .
.
由题设知,![]() ,
,
∴![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
![]() 即
即![]() .
.
又![]() ,
,![]() ,
,
∴![]() .
.
(2)解 ∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ⊥平面
⊥平面![]() .
.
∴三棱锥![]() 的体积为
的体积为
![]() .
.
(3)∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,又
,又![]()
![]() 又
又![]() ,
,
![]()
又在正方形![]() 中
中
![]()
![]()
连结![]() ,
,![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入
 种黄瓜的年收入
种黄瓜的年收入 与投入
与投入 (单位:万元)满足
(单位:万元)满足 .设甲大棚的投入为
.设甲大棚的投入为 (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为 (单位:万元)
(单位:万元)(1)求
 的值;
的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益
 最大?
最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为
 ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为 ,而当年产销量相等。
,而当年产销量相等。(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
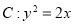 的焦点为
的焦点为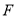 ,平行于
,平行于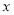 轴的两条直线
轴的两条直线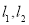 分别交
分别交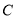 于
于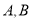 两点,交
两点,交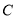 的准线于
的准线于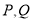 两点 .
两点 .(1)若
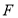 在线段
在线段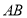 上,
上,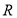 是
是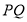 的中点,证明
的中点,证明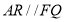 ;
;(2)若
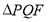 的面积是
的面积是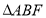 的面积的两倍,求
的面积的两倍,求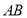 中点的轨迹方程.
中点的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆过点
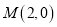 ,且被
,且被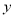 轴截得的线段长为4,记动圆圆心的轨迹为曲线
轴截得的线段长为4,记动圆圆心的轨迹为曲线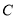 .
.(1)求曲线
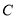 的方程;
的方程;(2)问:
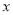 轴上是否存在一定点
轴上是否存在一定点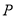 ,使得对于曲线
,使得对于曲线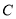 上的任意两点
上的任意两点 和
和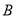 ,当
,当 时,恒有
时,恒有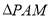 与
与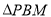 的面积之比等于
的面积之比等于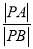 ?若存在,则求
?若存在,则求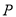 点的坐标,否则说明理由.
点的坐标,否则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱
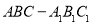 中,已知
中,已知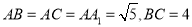 ,点
,点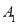 在底面
在底面 的投影是线段
的投影是线段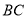 的中点
的中点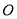 .
.
(1)证明:在侧棱
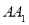 上存在一点
上存在一点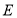 ,使得
,使得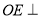 平面
平面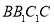 ,并求出
,并求出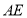 的长;
的长;(2)求:平面
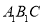 与平面
与平面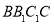 夹角的余弦值.
夹角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
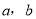 .
.(Ⅰ)求满足
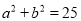 的概率;
的概率;(Ⅱ)设三条线段的长分别为
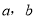 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
相关试题

