【题目】为保护农民种粮收益,促进粮食生产,确保国家粮食安全,调动广大农民粮食生产的积极性,从2004年开始,国家实施了对种粮农民直接补贴.通过对2014~2018年的数据进行调查,发现某地区发放粮食补贴额![]() (亿元)与该地区粮食产量
(亿元)与该地区粮食产量![]() (万亿吨)之间存在着线性相关关系.统计数据如下表:
(万亿吨)之间存在着线性相关关系.统计数据如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据如表所给的数据,求出![]() 关于
关于![]() 的线性回归直线方程
的线性回归直线方程![]() ;
;
(2)通过对该地区粮食产量的分析研究,计划2019年在该地区发放粮食补贴额7亿元,请根据(1)中所得的线性回归直线方程,预测2019年该地区的粮食产量.
(参考公式: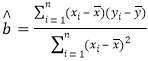 ,
,![]() )
)
参考答案:
【答案】(1)![]() (2)粮食产量大约为18.7万亿吨.
(2)粮食产量大约为18.7万亿吨.
【解析】
(1)由最小二乘法求出a,b的估计值,进而可得回归直线方程;
(2)将![]() 代入(1)所求的回归方程即可求出结果.
代入(1)所求的回归方程即可求出结果.
(1)由已知数据,可得![]() ,
,
![]() .
.
代入公式 ,经计算,得
,经计算,得![]() ,
,
∴![]() .
.
∴所求![]() 关于
关于![]() 的线性回归直线方程为
的线性回归直线方程为![]() .
.
(2)由题意,知![]() ,代入(1)中所得线性回归直线方程
,代入(1)中所得线性回归直线方程![]() ,计算得
,计算得![]() .
.
∴2019年该地区的粮食产量大约为18.7万亿吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,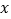 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程及曲线
的普通方程及曲线 的直角坐标方程;
的直角坐标方程;(2)已知点
 ,点
,点 ,直线
,直线 过点
过点 且与曲线
且与曲线 相交于
相交于 ,
, 两点,设线段
两点,设线段 的中点为
的中点为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近8年“双十一”期间的宣传费用
 (单位:万元)和利润
(单位:万元)和利润 (单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
(单位:十万元)之间的关系,搜集了相关数据,得到下列表格:
















(1)请用相关系数
 说明
说明 与
与 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当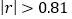 时,说明
时,说明 与
与 之间具有线性相关关系);
之间具有线性相关关系);(2)建立
 关于
关于 的线性回归方程(系数精确到
的线性回归方程(系数精确到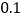 ),预测当宣传费用为
),预测当宣传费用为 万元时的利润,
万元时的利润,附参考公式:回归方程
 中
中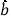 和
和 最小二乘估计公式分别为
最小二乘估计公式分别为 ,
, ,相关系数
,相关系数
参考数据:
 ,
,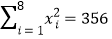 ,
, ,
,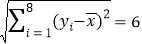
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以坐标原点为极点,
为参数).以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程及曲线
的普通方程及曲线 的直角坐标方程;
的直角坐标方程;(2)已知点
 ,点
,点 ,直线
,直线 过点
过点 且与曲线
且与曲线 相交于
相交于 ,
, 两点,设线段
两点,设线段 的中点为
的中点为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为


(1)求频率分布直方图中
 的值;
的值;(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在
 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,
, 是
是 的中点,以
的中点,以 为折痕将
为折痕将 向上折起,
向上折起, 变为
变为 ,且平面
,且平面 平面
平面 .
.
(Ⅰ)求证:
 ;
;(Ⅱ)求点
 到平面
到平面 的距离
的距离 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数

 一段图象如图所示。
一段图象如图所示。
(1)求出函数
 的解析式;
的解析式; (2) 函数
 的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到?
的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到? (3) 求出
 的单调递增区间;
的单调递增区间;(4) 指出当
 取得最小值时
取得最小值时 的集合.
的集合.
相关试题

