【题目】【2015高考广东,文19】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() ,且当
,且当![]()
时,![]() .
.
(1)求![]() 的值;
的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列![]() 的通项公式.
的通项公式.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)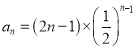 .
.
【解析】
试题分析:(1)令![]() 可得
可得![]() 的值;(2)先将
的值;(2)先将![]() (
(![]() )转化为
)转化为![]() ,再利用等比数列的定义可证
,再利用等比数列的定义可证![]() 是等比数列;(3)先由(2)可得数列
是等比数列;(3)先由(2)可得数列![]() 的通项公式,再将数列
的通项公式,再将数列![]() 的通项公式转化为数列
的通项公式转化为数列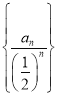 是等差数列,进而可得数列
是等差数列,进而可得数列![]() 的通项公式.
的通项公式.
试题解析:(1)当![]() 时,
时,![]() ,即
,即![]() ,解得:
,解得:![]()
(2)因为![]() (
(![]() ),所以
),所以![]() (
(![]() ),即
),即![]() (
(![]() ),因为
),因为![]() ,所以
,所以![]() ,因为
,因为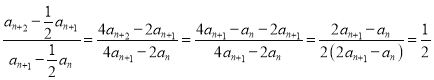 ,所以数列
,所以数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列
的等比数列
(3)由(2)知:数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,所以
的等比数列,所以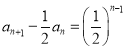
即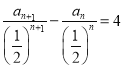 ,所以数列
,所以数列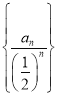 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,所以
的等差数列,所以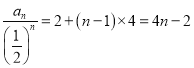 ,即
,即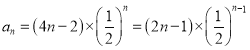 ,所以数列
,所以数列![]() 的通项公式是
的通项公式是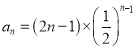
-
科目: 来源: 题型:
查看答案和解析>>【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电
 度时,应交电费
度时,应交电费 元,写出
元,写出 关于
关于 的函数关系式;
的函数关系式;(Ⅱ)小明家第一季度缴纳电费情况如下:
月份
一月
二月
三月
合计
交费金额
76元
63元
45.6元
184.6元
问小明家第一季度共用电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).(I)写出直线
 的一般方程与曲线
的一般方程与曲线 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;(II)将曲线
 向左平移
向左平移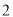 个单位长度,向上平移
个单位长度,向上平移 个单位长度,得到曲线
个单位长度,得到曲线 ,设曲线
,设曲线 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线 ,设曲线
,设曲线 上任一点为
上任一点为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届江苏如东高级中学等四校高三12月联考】已知数列
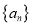 满足
满足 ,
,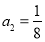 ,且对任意
,且对任意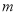 ,
,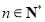 都有
都有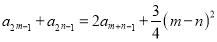 .
.(1)求
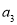 ,
,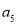 ;
;(2)设
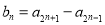 (
(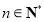 ).
).①求数列
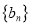 的通项公式;
的通项公式;②设数列
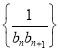 的前
的前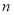 项和
项和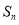 ,是否存在正整数
,是否存在正整数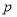 ,
,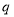 ,且
,且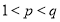 ,使得
,使得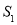 ,
, ,
,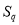 成等比数列?若存在,求出
成等比数列?若存在,求出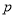 ,
,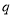 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修
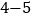 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
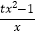
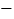 (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>
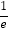 ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考四川文科】已知数列{
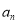 }的首项为1,
}的首项为1,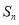 为数列
为数列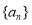 的前n项和,
的前n项和,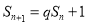 ,其中q>0,
,其中q>0, .
.(Ⅰ)若
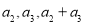 成等差数列,求
成等差数列,求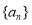 的通项公式;
的通项公式;(Ⅱ)设双曲线
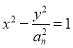 的离心率为
的离心率为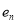 ,且
,且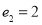 ,求
,求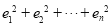 .
.
相关试题

