【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
参考答案:
【答案】(1)![]() ;(2)330度.
;(2)330度.
【解析】试题分析:(1)由题意可知![]() 关于
关于![]() 的函数关系式为分段函数,而且是关于
的函数关系式为分段函数,而且是关于![]() 的一次方程.由题意易得此方程.(2)当
的一次方程.由题意易得此方程.(2)当![]() 时,
时, ![]() ,由表可知小明家只有三月份用电小于100度,其他两个月均超过100度.将各月电费金额代入相应解析式即可求得当月用电量.
,由表可知小明家只有三月份用电小于100度,其他两个月均超过100度.将各月电费金额代入相应解析式即可求得当月用电量.
试题解析:(1)当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
所以所求函数式为
![]()
(2)据题意,
一月份: ![]() ,得
,得![]() (度),
(度),
二月份: ![]() ,得
,得![]() (度),
(度),
三月份: ![]() ,得
,得![]() (度).
(度).
所以第一季度共用电:
![]() (度).
(度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数
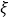 的概率分布列及期望.
的概率分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
 ﹣p
﹣p④回归直线一定过样本点的中心(
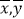 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数
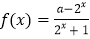 是奇函数
是奇函数(1)求
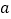 的值
的值(2)判断f(x)在
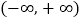 上的单调性。(直接写出答案,不用证明)
上的单调性。(直接写出答案,不用证明)(3)若对于任意
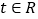 ,不等式
,不等式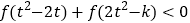 恒成立,求
恒成立,求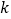 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).(I)写出直线
 的一般方程与曲线
的一般方程与曲线 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;(II)将曲线
 向左平移
向左平移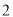 个单位长度,向上平移
个单位长度,向上平移 个单位长度,得到曲线
个单位长度,得到曲线 ,设曲线
,设曲线 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线 ,设曲线
,设曲线 上任一点为
上任一点为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届江苏如东高级中学等四校高三12月联考】已知数列
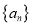 满足
满足 ,
,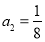 ,且对任意
,且对任意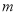 ,
,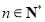 都有
都有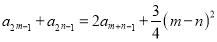 .
.(1)求
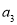 ,
,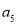 ;
;(2)设
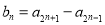 (
(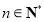 ).
).①求数列
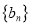 的通项公式;
的通项公式;②设数列
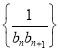 的前
的前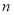 项和
项和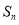 ,是否存在正整数
,是否存在正整数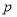 ,
,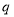 ,且
,且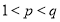 ,使得
,使得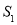 ,
, ,
,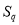 成等比数列?若存在,求出
成等比数列?若存在,求出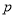 ,
,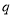 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2015高考广东,文19】设数列
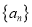 的前
的前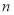 项和为
项和为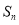 ,
, .已知
.已知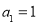 ,
,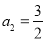 ,
,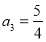 ,且当
,且当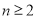
时,
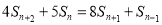 .
.(1)求
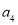 的值;
的值;(2)证明:
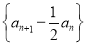 为等比数列;
为等比数列;(3)求数列
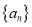 的通项公式.
的通项公式.
相关试题

