【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
参考答案:
【答案】(1)见解析(2)1
【解析】试题分析:(1)当![]() 时,对
时,对![]() 求导,
求导, ![]() 得增区间,
得增区间,![]() 得减区间,进而求出函数的最小值值,即可证明;(2)若t>
得减区间,进而求出函数的最小值值,即可证明;(2)若t>![]() ,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
试题解析:解:(1)t=1时,f(x)=x﹣![]() ﹣2lnx,x>0
﹣2lnx,x>0
∴f′(x)=1+![]() ﹣
﹣![]() =
=![]() =
=![]() ≥0,
≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1﹣1﹣0=0,
∴x>1,f(x)>0成立,
(2)当x∈(0,+∞),g(x)=tx2﹣(t+1)xlnx+(t+1)x﹣1
∴g′(x)=2tx﹣(t+1)lnx,
设m(x)=2tx﹣(t+1)lnx, ∴m′(x)=2t﹣![]() =
=![]() ,
,
令m′(x)=0,得x=![]() ,
,
当0<x<![]() 时,m'(x)<0;当时x>
时,m'(x)<0;当时x>![]() ,m'(x)>0.
,m'(x)>0.
∴g'(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴g'(x)的最小值为g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() ),
),
∵t>![]() ,∴
,∴![]() =
=![]() +
+![]() <
<![]() +
+![]() <e.
<e.
∴g'(x)的最小值g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() )>0,
)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g(1)=2t>0,又g(![]() )=
)=![]() +
+![]() (6+2lnt)﹣1,
(6+2lnt)﹣1,
设h(t)=e3t﹣(2lnt+6).
则h′(t)=e3﹣![]() .
.
令h'(t)=0得t=![]() .由h'(t)<0,得0<t<
.由h'(t)<0,得0<t<![]() ;
;
由h'(t)>0,得t>![]() .
.
∴h(t)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴h(t)min=h(![]() )=2﹣2ln2>0.
)=2﹣2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g(![]() )<
)<![]() +
+![]() ﹣1=
﹣1=![]() +
+![]() +
+![]() ﹣1<
﹣1<![]() +
+![]() +
+![]() ﹣1<0.
﹣1<0.
∴当t>![]() 时,函数g(x)恰有1个零点
时,函数g(x)恰有1个零点
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届江苏如东高级中学等四校高三12月联考】已知数列
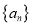 满足
满足 ,
,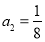 ,且对任意
,且对任意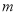 ,
,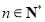 都有
都有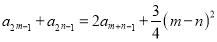 .
.(1)求
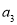 ,
,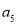 ;
;(2)设
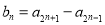 (
(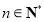 ).
).①求数列
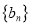 的通项公式;
的通项公式;②设数列
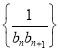 的前
的前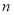 项和
项和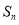 ,是否存在正整数
,是否存在正整数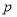 ,
,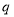 ,且
,且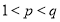 ,使得
,使得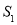 ,
, ,
,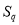 成等比数列?若存在,求出
成等比数列?若存在,求出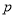 ,
,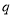 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2015高考广东,文19】设数列
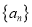 的前
的前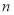 项和为
项和为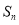 ,
, .已知
.已知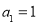 ,
,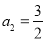 ,
,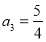 ,且当
,且当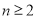
时,
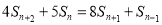 .
.(1)求
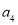 的值;
的值;(2)证明:
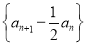 为等比数列;
为等比数列;(3)求数列
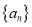 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修
 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考四川文科】已知数列{
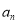 }的首项为1,
}的首项为1,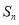 为数列
为数列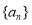 的前n项和,
的前n项和,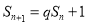 ,其中q>0,
,其中q>0, .
.(Ⅰ)若
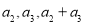 成等差数列,求
成等差数列,求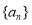 的通项公式;
的通项公式;(Ⅱ)设双曲线
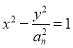 的离心率为
的离心率为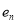 ,且
,且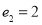 ,求
,求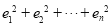 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
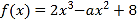 .
.(1)若
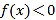 对
对 恒成立,求实数
恒成立,求实数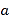 的取值范围;
的取值范围;(2)是否存在整数
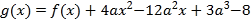 ,使得函数
,使得函数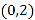 在区间
在区间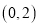 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数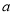 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|y=
 },B={x|x2-x-6=0}.
},B={x|x2-x-6=0}.(1)若a=-1,求A∩B;
(2)若(
 )∩B=,求实数a的取值范围.
)∩B=,求实数a的取值范围.
相关试题

