【题目】如图,三棱柱![]() -
-![]() 的底面是边长为2的等边三角形,
的底面是边长为2的等边三角形,![]() 底面
底面![]() ,点
,点![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,且
上的点,且![]()
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
参考答案:
【答案】(Ⅰ)证明过程见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,证得
,证得![]() 平面
平面![]() .
.
在根据三角形中位线定理,证得![]() ,得
,得![]()
![]() ,即可证得平面
,即可证得平面![]() 平面
平面![]()
(2)由(Ⅰ)可知,![]() ,再由
,再由![]() ,即可求解点
,即可求解点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,因为
,因为![]() 底面
底面![]() ,
,
所以侧面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,所以
,所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.

(Ⅱ)由(Ⅰ)可知,![]() 平面
平面![]() ,连接
,连接![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,
,
因为![]() ,依题意得
,依题意得![]() ,所以
,所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() ,得
,得![]() ,
,
即![]() ,所以
,所以![]()
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式ax2+5x﹣2>0的解集是
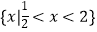 ,
,
(1)求实数a的值;
(2)求不等式ax2﹣5x+a2﹣1>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边长分别是a,b,c.
(1)若c=2,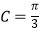 ,且△ABC的面积
,且△ABC的面积 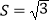 ,求a,b的值;
,求a,b的值;
(2)若sinC+sin(B﹣A)=sin2A,试判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an=
 (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= 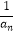 (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
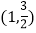 是椭圆E:
是椭圆E: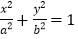 (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为 .
.(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
 的直线与抛物线相交于A,B两点.
的直线与抛物线相交于A,B两点.(1)用p表示线段AB的长;
(2)若
 ,求这个抛物线的方程.
,求这个抛物线的方程.
相关试题

