【题目】若不等式ax2+5x﹣2>0的解集是 ![]() ,
,
(1)求实数a的值;
(2)求不等式ax2﹣5x+a2﹣1>0的解集.
参考答案:
【答案】
(1)解:∵ax2+5x﹣2>0的解集是 ![]() ,
,
∴a<0, ![]() ,2是ax2+5x﹣2=0的两根
,2是ax2+5x﹣2=0的两根
解得 a=﹣2;
(2)解:则不等式ax2﹣5x+a2﹣1>0可化为
﹣2x2﹣5x+3>0
解得 ![]()
故不等式ax2﹣5x+a2﹣1>0的解集 ![]() .
.
【解析】(1)由二次不等式的解集形式,判断出 ![]() ,2是相应方程的两个根,利用韦达定理求出a的值.(2)由(1)我们易得a的值,代入不等式ax2﹣5x+a2﹣1>0易解出其解集.
,2是相应方程的两个根,利用韦达定理求出a的值.(2)由(1)我们易得a的值,代入不等式ax2﹣5x+a2﹣1>0易解出其解集.
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程
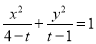 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4且t≠
 ;
;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<
 .
.其中正确的命题是________(把所有正确命题的序号都填在横线上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)已知
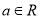 ,函数
,函数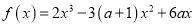
(Ⅰ)若
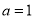 ,求曲线
,求曲线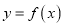 在点
在点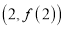 处的切线方程.
处的切线方程.(Ⅱ)若
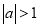 ,求
,求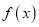 在闭区间
在闭区间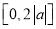 上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C所对的边长分别是a,b,c.
(1)若c=2,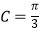 ,且△ABC的面积
,且△ABC的面积 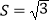 ,求a,b的值;
,求a,b的值;
(2)若sinC+sin(B﹣A)=sin2A,试判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
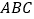 -
-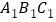 的底面是边长为2的等边三角形,
的底面是边长为2的等边三角形,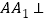 底面
底面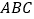 ,点
,点 分别是棱
分别是棱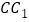 ,
,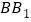 上的点,且
上的点,且
(1)证明:平面
 平面
平面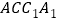 ;
;(2)若
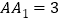 ,求点
,求点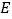 到平面
到平面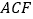 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an=
 (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= 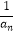 (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
相关试题

