【题目】过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为![]() 的直线与抛物线相交于A,B两点.
的直线与抛物线相交于A,B两点.
(1)用p表示线段AB的长;
(2)若![]() ,求这个抛物线的方程.
,求这个抛物线的方程.

参考答案:
【答案】(1)4p(2)y2=4x.
【解析】试题分析:(1)先根据点斜式写出直线方程,再与抛物线联立方程组,利用韦达定理得两根之和,最后根据抛物线定义求线段AB的长;(2)先根据向量数量积化简![]() ,再根据点斜式设直线方程,与抛物线联立方程组,利用韦达定理代入关系式,解出p
,再根据点斜式设直线方程,与抛物线联立方程组,利用韦达定理代入关系式,解出p
试题解析:解:(1)抛物线的焦点为F![]() ,过点F且倾斜角为
,过点F且倾斜角为![]() 的直线方程是y=x-
的直线方程是y=x-![]() .设A(x1,y1),B(x2,y2),联立
.设A(x1,y1),B(x2,y2),联立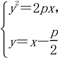
得x2-3px+![]() =0,∴x1+x2=3p,x1x2=
=0,∴x1+x2=3p,x1x2=![]() ,∴AB=x1+x2+p=4p.
,∴AB=x1+x2+p=4p.
(2)由(1)知x1x2=![]() ,x1+x2=3p,
,x1+x2=3p,
∴y1y2=![]()
![]() =x1x2-
=x1x2-![]() (x1+x2)+
(x1+x2)+![]() =
=![]() -
-![]() +
+![]() =-p2,
=-p2,
∴OA―→·OB―→=x1x2+y1y2=![]() -p2=-
-p2=-![]() =-3,
=-3,
解得p2=4,
∴p=2.
∴这个抛物线的方程为y2=4x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 -
- 的底面是边长为2的等边三角形,
的底面是边长为2的等边三角形, 底面
底面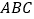 ,点
,点 分别是棱
分别是棱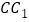 ,
,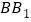 上的点,且
上的点,且
(1)证明:平面
 平面
平面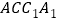 ;
;(2)若
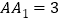 ,求点
,求点 到平面
到平面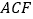 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an=
 (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= 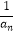 (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
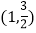 是椭圆E:
是椭圆E: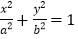 (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为 .
.(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
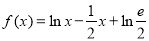 ,
,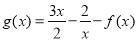 .
.(1)求
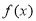 的单调区间;
的单调区间;(2)设函数
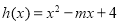 ,若存在
,若存在 ,对任意的
,对任意的 ,总有
,总有 成立,求实数
成立,求实数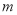 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
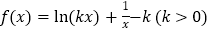 .
.(Ⅰ)求
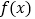 的单调区间;
的单调区间;(Ⅱ)对任意
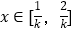 ,都有
,都有 ,求
,求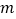 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程
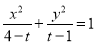 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4且t≠
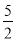 ;
;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<
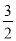 .
.其中正确的命题是________(把所有正确命题的序号都填在横线上).
相关试题

