【题目】已知函数f(x)=loga![]() (a>0且a≠1).
(a>0且a≠1).
(1)求f(x)的定义域;
(2)当0<a<1时,判断f(x)在(2,+∞)的单惆性;
(3)是否存在实数a,使得当f(x)的定义域为[m,n]时,值域为[1+logan,1+1ogam],若存在,求出实数a的范围;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ; (2)见解析;(3)存在这样的实数a∈(0,
; (2)见解析;(3)存在这样的实数a∈(0,![]() )符合题意.
)符合题意.
【解析】
(1)由对数式的真数大于0求解函数的定义域;
(2)利用分离常数法判断真数![]() 的单调性,再由复合函数的单调性得答案;
的单调性,再由复合函数的单调性得答案;
(3)把![]() 的定义域为
的定义域为![]() ,
,![]() 时值域为
时值域为![]() ,
,![]() 转化为
转化为![]() 在
在![]() 上为减函数,进一步得到
上为减函数,进一步得到![]() 在
在![]() 上有两个互异实根,令
上有两个互异实根,令![]() ,转化为关于
,转化为关于![]() 的不等式组求解.
的不等式组求解.
(1)由![]() >0,得x<-2或x>2.
>0,得x<-2或x>2.
∴f(x)的定义域为(-∞,-2)∪(2,+∞);
(2)令t(x)=![]() =1-
=1-![]() ,t(x)在(2,+∞)上为增函数,
,t(x)在(2,+∞)上为增函数,
又0<a<1,
∴f(x)在(2,+∞)上为减函数;
(3)假设存在这样的实数a,使得当f(x)的定义域为[m,n]时,值域为[1+logan,1+1ogam],
由m<n且1+logan,1+1ogam,
即m<n1+logan,1+1ogam,可得0<a<1.
t(x)=1-![]() 在(2,+∞)上为增函数,
在(2,+∞)上为增函数,
又∵0<a<1,
∴f(x)在(2,+∞)上为减函数,
∴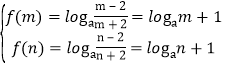 ,
,
∴![]() ,即
,即![]() 在(2,+∞)上有两个互异实根,
在(2,+∞)上有两个互异实根,
令g(x)=ax2+(2a-1)x+2,
则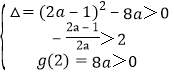 ,解得0<a<
,解得0<a<![]() .
.
又∵0<a<1,故存在这样的实数a∈(0,![]() )符合题意.
)符合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b∈R,c∈[0,2π),若对于任意实数x都有2sin(3x﹣
 )=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 .
)=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设an=1+
 +=
+= +…+
+…+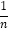 (n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论.
(n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是圆柱OO′的轴截面,点P在圆柱OO′的底面圆周上,圆柱OO′的底面圆的半径OA=1,侧面积为2π,∠AOP=60°.

(1)求证:PB⊥平面APD;
(2)是否存在点G在PD上,使得AG⊥BD;并说明理由.
(3)求三棱锥D-AGB的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n为正整数,试比较n2与2n的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)满足:①对于任意实数x,y都有f(x+y)+1=f(x)+f(x)且f(
 )=0;②当x>
)=0;②当x> 时,f(x)<0.
时,f(x)<0.(1)求证:f(x)=
 +
+ f(2x);
f(2x);(2)用数学归纳法证明:当x∈[
 ,
, ](n∈N*)时, f(x)≤1-
](n∈N*)时, f(x)≤1- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知
 的顶点
的顶点 ,若其欧拉线方程为
,若其欧拉线方程为 ,则顶点C的坐标是()
,则顶点C的坐标是()A.
 B.
B. 
C.
 D.
D. 
相关试题

