【题目】有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定:大桥上的车距d(m)与车速v(km/h)和车身长l(m)的关系满足:d=kv2l+ ![]() l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
参考答案:
【答案】
(1)解:因为当v=60时,d=2.66l,所以 ![]() ,
,
∴d=0.0024v2+2
(2)解:设每小时通过的车辆为Q,每小时内通过汽车的数量为Q最大,只须 ![]() 最小,
最小,
即Q= ![]()
∵ ![]() ,
,
当且仅当 ![]() ,即v=50时,Q取最大值
,即v=50时,Q取最大值 ![]() .
.
答:当v=50(km/h)时,大桥每小时通过的车辆最多
【解析】(1)根据当车速为60(km/h)时,车距为2.66个车身长,建立等式关系,求出k的值,即可求出车距d关于车速v的函数关系式;(2)设每小时通过的车辆为Q,每小时内通过汽车的数量为Q最大,只须 ![]() 最小,将d代入,然后利用基本不等式求出最值,即可求出所求.
最小,将d代入,然后利用基本不等式求出最值,即可求出所求.
【考点精析】解答此题的关键在于理解基本不等式的相关知识,掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内给定三个向量
 =(3,2),
=(3,2), 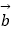 =(﹣1,2),
=(﹣1,2),  =(4,1).回答下列问题:
=(4,1).回答下列问题:
(1)若( +k
+k  )∥(2
)∥(2 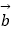 ﹣
﹣  ),求实数k;
),求实数k;
(2)设 =(x,y)满足(
=(x,y)满足(  ﹣
﹣  )∥(
)∥(  +
+ 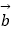 )且|
)且|  ﹣
﹣  |=1,求
|=1,求  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的偶函数f(x)满足对于任意实数x,都有f(1+x)=f(1﹣x),且当0≤x≤1时,f(x)=3x+1 .
(1)求证:函数f(x)是周期函数;
(2)当x∈[1,3]时,求f(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=sin(ωx+φ)(ω>0,|φ|<
 )在同一个周期内,当x=
)在同一个周期内,当x=  时y取最大值1,当x=
时y取最大值1,当x= 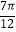 时y取最小值﹣1.
时y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)当x∈[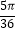 ,
, 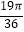 ]时.求函数y=f(x)的值域.
]时.求函数y=f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
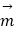 =(2cos2x,sinx),
=(2cos2x,sinx),  =(1,2cosx). (Ⅰ)若
=(1,2cosx). (Ⅰ)若 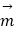 ⊥
⊥  且0<x<π,试求x的值;
且0<x<π,试求x的值;
(Ⅱ)设f(x)=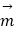
 ,试求f(x)的对称轴方程和对称中心.
,试求f(x)的对称轴方程和对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正四面体ABCD中,
 是
是 的中心,
的中心,  分别是
分别是 上的动点,且
上的动点,且 .
.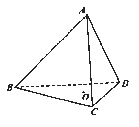
(1)若
 平面
平面 ,求实数
,求实数 的值;
的值;(2)若
 ,正四面体ABCD的棱长为
,正四面体ABCD的棱长为 ,求平面
,求平面 和平面
和平面 所成的角余弦值.
所成的角余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).
(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
相关试题

