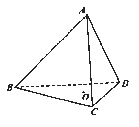
【题目】如图,在正四面体ABCD中, ![]() 是
是![]() 的中心,
的中心, ![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() .
.
(1)若![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,正四面体ABCD的棱长为
,正四面体ABCD的棱长为![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角余弦值.
所成的角余弦值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)本问主要考查线面平行性质定理的应用,若![]() 平面
平面![]() ,那么经过OE的平面与平面ACD相交,则OE平行于交线,因此需要找到经过OE的平面,由
,那么经过OE的平面与平面ACD相交,则OE平行于交线,因此需要找到经过OE的平面,由![]() 是正
是正![]() 的中心,易知O为BC的三等分点,因此能确定E点位置;(2)本问主要考查用空间向量求二面角问题,当
的中心,易知O为BC的三等分点,因此能确定E点位置;(2)本问主要考查用空间向量求二面角问题,当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点,以O为原点,过O作CD的垂线为x轴,过O作BC的垂线为y轴,OA为z轴,建立空间直角直角坐标系,则易得出下列各点坐标
的中点,以O为原点,过O作CD的垂线为x轴,过O作BC的垂线为y轴,OA为z轴,建立空间直角直角坐标系,则易得出下列各点坐标![]() ,
,  ,由此求出相关向量的坐标,再分别求出平面
,由此求出相关向量的坐标,再分别求出平面![]() 和平面
和平面![]() 的法向量,根据两个平面的法向量可以求夹角的余弦,再由图观察向量成角的余弦与二面角余弦之间的关系即可.
的法向量,根据两个平面的法向量可以求夹角的余弦,再由图观察向量成角的余弦与二面角余弦之间的关系即可.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,

∵![]() 是正
是正![]() 的中心 ∴点
的中心 ∴点![]() 在
在![]() 上,且
上,且![]() ,
,
∵当![]() 时,
时,![]() 平面
平面 ![]() ,
,
∴![]() ∴
∴![]() ,即
,即![]() ,
,
∴![]() .
.
(2)当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点.
的中点.
建立如图所示的空间直角坐标系![]() ,依题设
,依题设
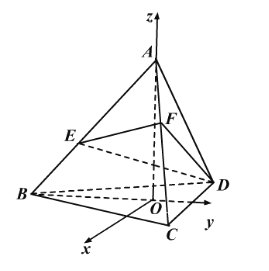
![]() ,则
,则![]() ,
,  ,
,
则 ,
,
设平面![]() 的法向量为
的法向量为![]() 则
则 ,
,
∴ ,
,
不妨令![]() ,则
,则 ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() .
.
设所求二面角为![]() ,则
,则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=sin(ωx+φ)(ω>0,|φ|<
 )在同一个周期内,当x=
)在同一个周期内,当x=  时y取最大值1,当x=
时y取最大值1,当x= 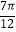 时y取最小值﹣1.
时y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)当x∈[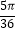 ,
, 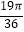 ]时.求函数y=f(x)的值域.
]时.求函数y=f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定:大桥上的车距d(m)与车速v(km/h)和车身长l(m)的关系满足:d=kv2l+
 l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
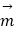 =(2cos2x,sinx),
=(2cos2x,sinx),  =(1,2cosx). (Ⅰ)若
=(1,2cosx). (Ⅰ)若 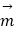 ⊥
⊥  且0<x<π,试求x的值;
且0<x<π,试求x的值;
(Ⅱ)设f(x)=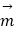
 ,试求f(x)的对称轴方程和对称中心.
,试求f(x)的对称轴方程和对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).
(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用寒假进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数
分组
低碳族人数
占本组的频率
第一组
[25,30)
120
0.6
第二组
[30,35)
195
p
第三组
[35,40)
100
0.5
第四组
[40,45)
a
0.4
第五组
[45,50)
30
0.3
第六组
[50,55)
15
0.3

(1)补全频率分布直方图并求n、a、p的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=a分别与曲线y=2(x+1),y=x+lnx交于A、B,则|AB|的最小值为( )
A.3
B.2
C.
D.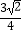
相关试题

