【题目】已知定义域为R的偶函数f(x)满足对于任意实数x,都有f(1+x)=f(1﹣x),且当0≤x≤1时,f(x)=3x+1 .
(1)求证:函数f(x)是周期函数;
(2)当x∈[1,3]时,求f(x)的解析式.
参考答案:
【答案】
(1)解:对任意实数x都有
f(x+2)=f[1+(1+x)]=f[1﹣(1+x)]=f(﹣x),
由于f(x)为偶函数,f(﹣x)=f(x)
∴f(x+2)=f(x)
∴函数f(x)是以2为周期的周期函数
(2)解:当x∈[1,2]时,2﹣x∈[0,1]
则f(x)=f(﹣x)=f(2﹣x)=32﹣x+1=33﹣x,
当x∈[2,3]时,x﹣2∈[0,1]
则f(x)=f(x﹣2)=3x﹣2+1=3x﹣1,
综上,f(x)= ![]()
【解析】把x+2拆成1+(x+1),代入f(1+x)=f(1﹣x),再利用偶函数的性质f(﹣x)=f(x)推导周期.(2)利用第(1)问中函数的周期及奇偶性过度到已知区间上函数的表达式求解函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设常数
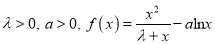 .
.(1)若
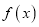 在
在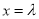 处取得极小值为
处取得极小值为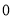 ,求
,求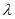 和
和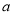 的值;
的值;(2)对于任意给定的正实数
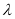 、
、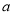 ,证明:存在实数
,证明:存在实数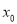 ,当
,当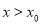 时,
时, 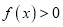 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x),将f(x)图像沿x轴向右平移
 个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣
个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣  )的图像相同,那么y=f(x)的解析式为( )
)的图像相同,那么y=f(x)的解析式为( )
A.f(x)=2sin(2x﹣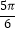 )
)
B.f(x)=2sin(2x﹣ )
)
C.f(x)=2sin(2x+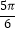 )
)
D.f(x)=2sin(2x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】平面内给定三个向量
 =(3,2),
=(3,2), 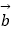 =(﹣1,2),
=(﹣1,2),  =(4,1).回答下列问题:
=(4,1).回答下列问题:
(1)若( +k
+k  )∥(2
)∥(2 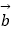 ﹣
﹣  ),求实数k;
),求实数k;
(2)设 =(x,y)满足(
=(x,y)满足(  ﹣
﹣  )∥(
)∥(  +
+ 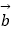 )且|
)且|  ﹣
﹣  |=1,求
|=1,求  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=sin(ωx+φ)(ω>0,|φ|<
 )在同一个周期内,当x=
)在同一个周期内,当x=  时y取最大值1,当x=
时y取最大值1,当x= 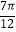 时y取最小值﹣1.
时y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)当x∈[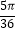 ,
, 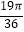 ]时.求函数y=f(x)的值域.
]时.求函数y=f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定:大桥上的车距d(m)与车速v(km/h)和车身长l(m)的关系满足:d=kv2l+
 l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
l(k为正的常数),假定大桥上的车的车身长都为4m,当车速为60km/h时,车距为2.66个车身长.
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
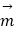 =(2cos2x,sinx),
=(2cos2x,sinx),  =(1,2cosx). (Ⅰ)若
=(1,2cosx). (Ⅰ)若 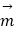 ⊥
⊥  且0<x<π,试求x的值;
且0<x<π,试求x的值;
(Ⅱ)设f(x)=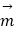
 ,试求f(x)的对称轴方程和对称中心.
,试求f(x)的对称轴方程和对称中心.
相关试题

