【题目】设![]() ,
,![]() 是双曲线C:
是双曲线C:![]() 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点![]() 过
过![]() 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若![]() ,则C的离心率为
,则C的离心率为![]()
![]()
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
先根据点到直线的距离求出|PF2|=b,再求出|OP|=a,在三角形F1PF2中,由余弦定理可得|PF1|2=|PF2|2+|F1F2|2﹣2|PF2||F1F2|cos∠PF2O,代值化简整理可得![]() a=c,问题得以解决.
a=c,问题得以解决.
双曲线C:![]() 1(a>0.b>0)的一条渐近线方程为y
1(a>0.b>0)的一条渐近线方程为y![]() x,
x,
∴点F2到渐近线的距离d![]() b,即|PF2|=b,
b,即|PF2|=b,
∴|OP|![]() a,cos∠PF2O
a,cos∠PF2O![]() ,
,
∵|PF1|![]() |OP|,
|OP|,
∴|PF1|![]() a,
a,
在三角形F1PF2中,由余弦定理可得|PF1|2=|PF2|2+|F1F2|2﹣2|PF2||F1F2|COS∠PF2O,
∴6a2=b2+4c2﹣2×b×2c![]() 4c2﹣3b2=4c2﹣3(c2﹣a2),
4c2﹣3b2=4c2﹣3(c2﹣a2),
即3a2=c2,
即![]() a=c,
a=c,
∴e![]() ,
,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如图数阵的表格形式,表格内是按某种规律排列成的有限个正整数.

(1)记第一行的自左至右构成数列
 ,
, 是
是 的前
的前 项和,试求
项和,试求 的表达式;
的表达式;(2)记
 为第
为第 行与第
行与第 列交点的数字,观察数阵,若
列交点的数字,观察数阵,若 ,试求出
,试求出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校
 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是 ,
, ,
, ,
, ,
, ,
, .
.
 求图中
求图中 的值;
的值; 根据频率分布直方图,估计这
根据频率分布直方图,估计这 名学生的平均分;
名学生的平均分; 若这
若这 名学生的数学成绩中,某些分数段的人数
名学生的数学成绩中,某些分数段的人数 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数 之比如表所示,求英语成绩在
之比如表所示,求英语成绩在 的人数.
的人数.分数段




 :5
:51:2
1:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 称为
称为 ,
, 的二维平方平均数,
的二维平方平均数,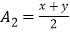 称为
称为 ,
, 的二维算术平均数,
的二维算术平均数, 称为
称为 ,
, 的二维几何平均数,
的二维几何平均数, 称为
称为 ,
, 的二维调和平均数,其中
的二维调和平均数,其中 ,
, 均为正数.
均为正数.(1)试判断
 与
与 的大小,并证明你的猜想.
的大小,并证明你的猜想.(2)令
 ,
, ,试判断
,试判断 与
与 的大小,并证明你的猜想.
的大小,并证明你的猜想.(3)令
 ,
, ,
, ,试判断
,试判断 、
、 、
、 三者之间的大小关系,并证明你的猜想.
三者之间的大小关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,其中实数
,其中实数 满足
满足 ,若
,若 的最大值为
的最大值为 ,则
,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆的中心在原点,焦点在
 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点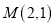 ,平行于
,平行于 的直线
的直线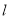 在
在 轴上的截距为
轴上的截距为 ,直线
,直线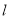 交椭圆于
交椭圆于 两个不同点.
两个不同点.
(1)求椭圆的方程;
(2)求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
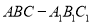 中,侧棱
中,侧棱 底面
底面 ,
,  为棱
为棱 中点.
中点. 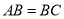 ,
,  ,
,  .
.
(I)求证:
 平面
平面 .
.(II)求证:
 平面
平面 .
.(III)在棱
 的上是否存在点
的上是否存在点 ,使得平面
,使得平面 平面
平面 ?如果存在,求此时
?如果存在,求此时 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
相关试题

