【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)函数![]() 是
是![]() 上的减函数 ;(2)见解析.
上的减函数 ;(2)见解析.
【解析】
(1)求出函数f(x)的定义域,并对函数f(x)求导,确定f′(x)的正负,即可确定函数f(x)在定义域上的单调性;(2)设a>b>0,分为两个不等式![]() 和
和![]() .证明不等式
.证明不等式![]() 时,转化为
时,转化为![]() ,换元t=
,换元t=![]() >1,转化为
>1,转化为![]() ,通过函数f(x)在区间(1,+∞)上的单调性来证明;证明不等式
,通过函数f(x)在区间(1,+∞)上的单调性来证明;证明不等式![]() ,转化为
,转化为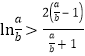 ,换元x=
,换元x=![]() >1,构造函数
>1,构造函数![]() ,通过函数g(x)在区间(1,+∞)的单调性来证明.
,通过函数g(x)在区间(1,+∞)的单调性来证明.
(1)函数f(x)的定义域为(0,+∞),![]() ,所以,函数f(x)在定义域(0,+∞)上单调递减;
,所以,函数f(x)在定义域(0,+∞)上单调递减;
(2)假设a>b>0.先证明不等式![]() ,即证
,即证![]() ,即证
,即证![]() ,令
,令![]() ,则原不等式即为
,则原不等式即为![]() ,其中t>1,由(1)知,函数f(x)在(0,+∞)上单调递减,当t>1时,f(t)<f(1)=0,即
,其中t>1,由(1)知,函数f(x)在(0,+∞)上单调递减,当t>1时,f(t)<f(1)=0,即
![]() ,即
,即![]() ,所以,当a>b>0时,
,所以,当a>b>0时,![]() .
.
下面证明![]() .即证
.即证![]() ,即
,即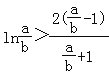 ,
,
令![]() ,即证
,即证![]() ,其中x>1,构造函数
,其中x>1,构造函数![]() ,其中x>1,
,其中x>1,![]() ,所以,函数g(x)在区间(1,+∞)上单调递增,所以,g(x)>g(1)=0,所以,当x>1时,
,所以,函数g(x)在区间(1,+∞)上单调递增,所以,g(x)>g(1)=0,所以,当x>1时,![]() ,
,
所以,当a>b>0时,![]() .
.
综上所述,当a>0,b>0时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
序号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
甲
×
96
93
×
92
×
90
86
×
×
83
80
78
77
75
乙
×
95
×
93
×
92
×
88
83
×
82
80
80
74
73
据表1中甲、乙两选手完成该项关键技能挑战成功所用时间的数据,应用统计软件得下表2:
数字特征
均值(单位:秒)方差
方差
甲
85
50.2
乙
84
54
(1)在表1中,从选手甲完成挑战用时低于90秒的成绩中,任取2个,求这2个成绩都低于80秒的概率;
(2)若该公司只有一个参赛名额,以该关键技能挑战成绩为标准,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, ,
,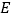 是棱
是棱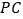 上的一点.
上的一点.(1)证明:
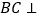 平面
平面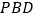 ;
; (2)若
 平面
平面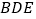 ,求
,求 的值;
的值;(3)在(2)的条件下,三棱锥
 的体积是18,求
的体积是18,求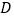 点到平面
点到平面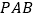 的距离.
的距离.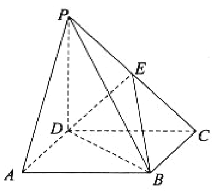
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为
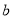 和
和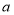 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为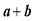 ,宽为内接正方形的边长
,宽为内接正方形的边长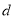 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设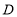 为斜边
为斜边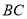 的中点,作直角三角形
的中点,作直角三角形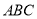 的内接正方形对角线
的内接正方形对角线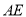 ,过点
,过点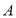 作
作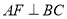 于点
于点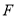 ,则下列推理正确的是( )
,则下列推理正确的是( )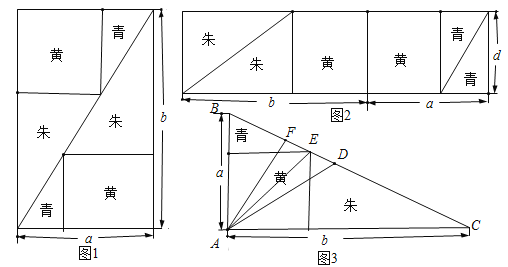
①由图1和图2面积相等得
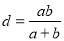 ;
;②由
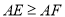 可得
可得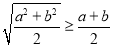 ;
;③由
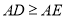 可得
可得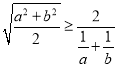 ;
;④由
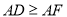 可得
可得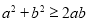 .
.A.①②③④B.①②④C.②③④D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人独立破译同一密码,甲破译密码的概率为
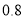 ,乙破译密码的概率为
,乙破译密码的概率为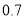 .记事件A:甲破译密码,事件B:乙破译密码.
.记事件A:甲破译密码,事件B:乙破译密码.(1)求甲、乙二人都破译密码的概率;
(2)求恰有一人破译密码的概率;
(3)小明同学解答“求密码被破译的概率”的过程如下:
解:“密码被破译”也就是“甲、乙二人中至少有一人破译密码”所以随机事件“密码被破译”可以表示为
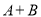 所以
所以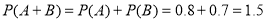
请指出小明同学错误的原因?并给出正确解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 )的图象过点
)的图象过点 ,
, .若函数
.若函数 在定义域内存在实数t,使得
在定义域内存在实数t,使得 成立,则称函数
成立,则称函数 具有性质M.
具有性质M.(1)求实数a的值;
(2)判断函数
 是否具有性质M?并说明理由;
是否具有性质M?并说明理由;(3)证明:函数
 具有性质M.
具有性质M. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
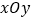 中,曲线
中,曲线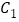 的参数方程为
的参数方程为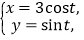 (
(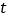 为参数).以原点为极点,
为参数).以原点为极点,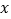 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线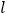 的极坐标方程为
的极坐标方程为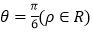 .
.(1)求
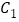 的极坐标方程;
的极坐标方程;(2)若曲线
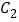 的极坐标方程为
的极坐标方程为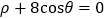 ,直线
,直线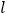 与
与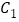 在第一象限的交点为
在第一象限的交点为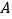 ,与
,与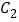 的交点为
的交点为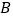 (异于原点),求
(异于原点),求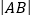 .
.
相关试题

