【题目】甲、乙二人独立破译同一密码,甲破译密码的概率为![]() ,乙破译密码的概率为
,乙破译密码的概率为![]() .记事件A:甲破译密码,事件B:乙破译密码.
.记事件A:甲破译密码,事件B:乙破译密码.
(1)求甲、乙二人都破译密码的概率;
(2)求恰有一人破译密码的概率;
(3)小明同学解答“求密码被破译的概率”的过程如下:
解:“密码被破译”也就是“甲、乙二人中至少有一人破译密码”所以随机事件“密码被破译”可以表示为![]() 所以
所以![]()
请指出小明同学错误的原因?并给出正确解答过程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)由相互独立事件概率乘法公式求解即可;
(2)恰有一人破译密码表示为![]() ,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解;
,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解;
(3)小明求解错误的原因是事件![]() 和事件
和事件![]() 不互斥,然后将甲、乙二人中至少有一人破译密码表示为
不互斥,然后将甲、乙二人中至少有一人破译密码表示为![]() ,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解.
,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解.
(1)由题意可知![]() ,
,![]() ,且事件A,B相互独立,
,且事件A,B相互独立,
事件“甲、乙二人都破译密码”可表示为![]() ,
,
所以![]() ;
;
(2)事件“恰有一人破译密码”可表示为![]() ,且
,且![]() ,
,![]() 互斥
互斥
所以![]()
![]()
(3)小明同学错误在于事件A,B不互斥,而用了互斥事件的概率加法公式
正确解答过程如下
“密码被破译”也就是“甲、乙二人中至少有一人破译密码”
可以表示为![]() ,且
,且![]() ,
,![]() ,
,![]() 两两互斥
两两互斥
所以![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面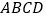 是平行四边形,
是平行四边形, 平面
平面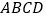 ,
, ,
, ,
,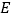 是棱
是棱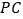 上的一点.
上的一点.(1)证明:
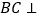 平面
平面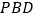 ;
; (2)若
 平面
平面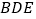 ,求
,求 的值;
的值;(3)在(2)的条件下,三棱锥
 的体积是18,求
的体积是18,求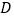 点到平面
点到平面 的距离.
的距离.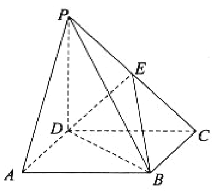
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为
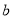 和
和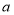 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为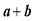 ,宽为内接正方形的边长
,宽为内接正方形的边长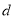 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设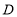 为斜边
为斜边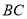 的中点,作直角三角形
的中点,作直角三角形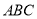 的内接正方形对角线
的内接正方形对角线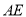 ,过点
,过点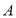 作
作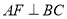 于点
于点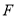 ,则下列推理正确的是( )
,则下列推理正确的是( )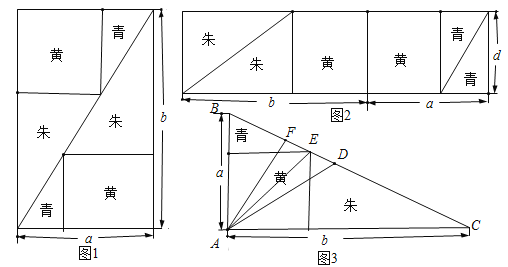
①由图1和图2面积相等得
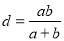 ;
;②由
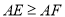 可得
可得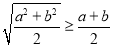 ;
;③由
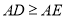 可得
可得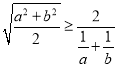 ;
;④由
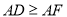 可得
可得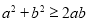 .
.A.①②③④B.①②④C.②③④D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
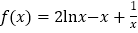 .
.(1)讨论
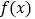 的单调性;
的单调性;(2)若
 ,
, ,证明:
,证明: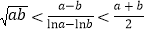 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 )的图象过点
)的图象过点 ,
, .若函数
.若函数 在定义域内存在实数t,使得
在定义域内存在实数t,使得 成立,则称函数
成立,则称函数 具有性质M.
具有性质M.(1)求实数a的值;
(2)判断函数
 是否具有性质M?并说明理由;
是否具有性质M?并说明理由;(3)证明:函数
 具有性质M.
具有性质M. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
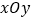 中,曲线
中,曲线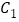 的参数方程为
的参数方程为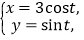 (
(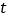 为参数).以原点为极点,
为参数).以原点为极点,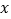 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线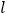 的极坐标方程为
的极坐标方程为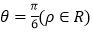 .
.(1)求
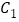 的极坐标方程;
的极坐标方程;(2)若曲线
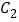 的极坐标方程为
的极坐标方程为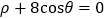 ,直线
,直线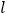 与
与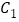 在第一象限的交点为
在第一象限的交点为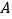 ,与
,与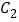 的交点为
的交点为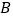 (异于原点),求
(异于原点),求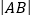 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数
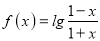 为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )
为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )A.同学甲发现:函数的定义域为(﹣1,1),且f(x)是偶函数
B.同学乙发现:对于任意的x∈(﹣1,1),都有

C.同学丙发现:对于任意的a,b∈(﹣1,1),都有
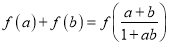
D.同学丁发现:对于函数定义域内任意两个不同的实数x1,x2,总满足
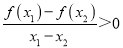
相关试题

