【题目】已知函数![]() (
(![]() 且
且![]() )的图象过点
)的图象过点![]() ,
,![]() .若函数
.若函数![]() 在定义域内存在实数t,使得
在定义域内存在实数t,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质M.
具有性质M.
(1)求实数a的值;
(2)判断函数![]() 是否具有性质M?并说明理由;
是否具有性质M?并说明理由;
(3)证明:函数![]() 具有性质M.
具有性质M.
参考答案:
【答案】(1)![]() ;(2)函数
;(2)函数![]() 不具有性质M,详见解析;(3)证明见解析
不具有性质M,详见解析;(3)证明见解析
【解析】
(1)将点![]() 代入
代入![]() 的解析式求解即可;
的解析式求解即可;
(2)由![]() ,可得对数方程,运用对数的性质判断方程的解,即可判断
,可得对数方程,运用对数的性质判断方程的解,即可判断![]() 是否具有性质
是否具有性质![]() ;
;
(3)由![]() ,求得方程的根或范围,结合新定义即可得证.
,求得方程的根或范围,结合新定义即可得证.
(1)由题意,函数![]() 的图象过点
的图象过点![]() ,
,
所以![]() ,解得
,解得![]() ;
;
(2)函数![]() 不具有性质M,证明如下:
不具有性质M,证明如下:
函数![]() 的定义域为
的定义域为![]() ,
,
方程![]()
![]() ,
,
而方程![]() 无解,
无解,
所以不存在实数![]() 使得
使得![]() 成立,
成立,
所以函数![]() 不具有性质M;
不具有性质M;
(3)由(1)知![]() ,定义域为R,
,定义域为R,
方程![]()
![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,
函数![]() 的图象连续,且
的图象连续,且![]() ,
,
所以函数![]() 在区间
在区间![]() 存在零点,
存在零点,
所以存在实数t使得![]() 成立,
成立,
所以函数![]() 具有性质M.
具有性质M.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为
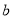 和
和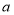 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为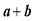 ,宽为内接正方形的边长
,宽为内接正方形的边长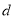 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设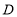 为斜边
为斜边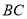 的中点,作直角三角形
的中点,作直角三角形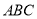 的内接正方形对角线
的内接正方形对角线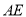 ,过点
,过点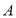 作
作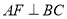 于点
于点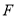 ,则下列推理正确的是( )
,则下列推理正确的是( )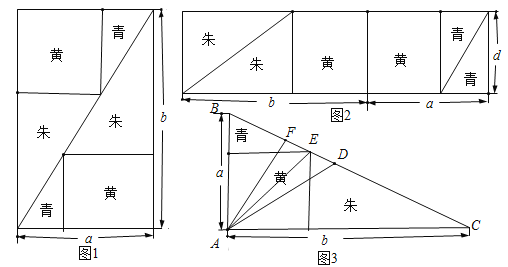
①由图1和图2面积相等得
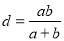 ;
;②由
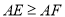 可得
可得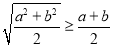 ;
;③由
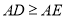 可得
可得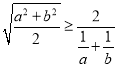 ;
;④由
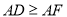 可得
可得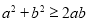 .
.A.①②③④B.①②④C.②③④D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
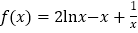 .
.(1)讨论
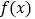 的单调性;
的单调性;(2)若
 ,
, ,证明:
,证明: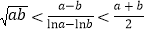 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人独立破译同一密码,甲破译密码的概率为
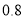 ,乙破译密码的概率为
,乙破译密码的概率为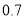 .记事件A:甲破译密码,事件B:乙破译密码.
.记事件A:甲破译密码,事件B:乙破译密码.(1)求甲、乙二人都破译密码的概率;
(2)求恰有一人破译密码的概率;
(3)小明同学解答“求密码被破译的概率”的过程如下:
解:“密码被破译”也就是“甲、乙二人中至少有一人破译密码”所以随机事件“密码被破译”可以表示为
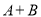 所以
所以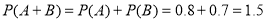
请指出小明同学错误的原因?并给出正确解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
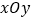 中,曲线
中,曲线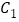 的参数方程为
的参数方程为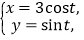 (
(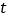 为参数).以原点为极点,
为参数).以原点为极点,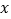 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线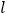 的极坐标方程为
的极坐标方程为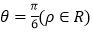 .
.(1)求
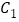 的极坐标方程;
的极坐标方程;(2)若曲线
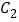 的极坐标方程为
的极坐标方程为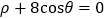 ,直线
,直线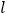 与
与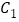 在第一象限的交点为
在第一象限的交点为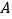 ,与
,与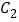 的交点为
的交点为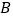 (异于原点),求
(异于原点),求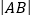 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数
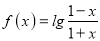 为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )
为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )A.同学甲发现:函数的定义域为(﹣1,1),且f(x)是偶函数
B.同学乙发现:对于任意的x∈(﹣1,1),都有

C.同学丙发现:对于任意的a,b∈(﹣1,1),都有
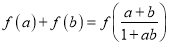
D.同学丁发现:对于函数定义域内任意两个不同的实数x1,x2,总满足
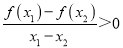
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数
未损坏餐椅数
总计
学习雷锋精神前
50
150
200
学习雷锋精神后
30
170
200
总计
80
320
400
 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关? 请说明是否有
请说明是否有 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神有关?
 参考公式:
参考公式: ,
,











相关试题

