【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() ,与
,与![]() 的交点为
的交点为![]() (异于原点),求
(异于原点),求![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接利用转换关系,把参数方程直角坐标方程和极坐标方程之间进行转换.(2)由极径的应用求出结果.
(1)曲线C1的参数方程为![]() (t为参数).
(t为参数).
转换为直角坐标方程为:![]() ,
,
转换为极坐标方程为:ρ2+8ρ2sin2θ﹣9=0.
(2)因为![]() ,
,![]() 两点在直线
两点在直线![]() 上,可设
上,可设![]() ,
,![]() .
.
把点![]() 的极坐标代入
的极坐标代入![]() 的方程得:
的方程得:![]() ,解得
,解得![]() .
.
由己知![]() 点在第一象限,所以
点在第一象限,所以![]() .
.
因为![]() 异于原点,所以把点
异于原点,所以把点![]() 的极坐标代入
的极坐标代入![]() 的方程得:
的方程得:
![]() ,解得
,解得![]() .
.
所以,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
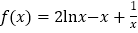 .
.(1)讨论
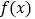 的单调性;
的单调性;(2)若
 ,
, ,证明:
,证明: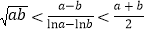 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人独立破译同一密码,甲破译密码的概率为
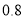 ,乙破译密码的概率为
,乙破译密码的概率为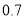 .记事件A:甲破译密码,事件B:乙破译密码.
.记事件A:甲破译密码,事件B:乙破译密码.(1)求甲、乙二人都破译密码的概率;
(2)求恰有一人破译密码的概率;
(3)小明同学解答“求密码被破译的概率”的过程如下:
解:“密码被破译”也就是“甲、乙二人中至少有一人破译密码”所以随机事件“密码被破译”可以表示为
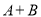 所以
所以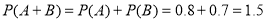
请指出小明同学错误的原因?并给出正确解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 )的图象过点
)的图象过点 ,
, .若函数
.若函数 在定义域内存在实数t,使得
在定义域内存在实数t,使得 成立,则称函数
成立,则称函数 具有性质M.
具有性质M.(1)求实数a的值;
(2)判断函数
 是否具有性质M?并说明理由;
是否具有性质M?并说明理由;(3)证明:函数
 具有性质M.
具有性质M. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数
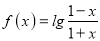 为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )
为基本素材,研究该函数的相关性质,取得部分研究成果如下:其中研究成果正确的是( )A.同学甲发现:函数的定义域为(﹣1,1),且f(x)是偶函数
B.同学乙发现:对于任意的x∈(﹣1,1),都有

C.同学丙发现:对于任意的a,b∈(﹣1,1),都有
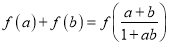
D.同学丁发现:对于函数定义域内任意两个不同的实数x1,x2,总满足
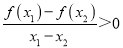
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数
未损坏餐椅数
总计
学习雷锋精神前
50
150
200
学习雷锋精神后
30
170
200
总计
80
320
400
 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关? 请说明是否有
请说明是否有 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神有关?
 参考公式:
参考公式: ,
,











-
科目: 来源: 题型:
查看答案和解析>>【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列结论正确的是( )
A.四面体ABCD每组对棱相互垂直
B.四面体ABCD每个面的面积相等
C.从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°且小于180°
D.连接四面体ABCD每组对棱中点的线段相互垂直平分
相关试题

