【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,若
,若![]() 是线段
是线段![]() 的中点,则双曲线的离心率是( )
的中点,则双曲线的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
双曲线的右焦点的坐标为(c,0),利用O为![]() 的中点,E为
的中点,E为![]() P的中点,可得OE为△P
P的中点,可得OE为△P![]() 的中位线,从而可求|P
的中位线,从而可求|P![]() |,再设P(x,y) 过点
|,再设P(x,y) 过点![]() 作x轴的垂线,由勾股定理得出关于a,c的关系式,最后即可求得离心率.
作x轴的垂线,由勾股定理得出关于a,c的关系式,最后即可求得离心率.
设双曲线的右焦点为![]() ,则
,则![]() 的坐标为(c,0)
的坐标为(c,0)
因为抛物线为y2=4cx,所以![]() 为抛物线的焦点
为抛物线的焦点
因为O为![]() 的中点,E为
的中点,E为![]() P的中点,所以OE为△P
P的中点,所以OE为△P![]() 的中位线,
的中位线,
属于OE∥P![]()
因为|OE|=a,所以|P![]() |=2a
|=2a
又P![]() ⊥P
⊥P![]() ,|
,|![]() |=2c 所以|P
|=2c 所以|P![]() |=2b
|=2b
设P(x,y),则由抛物线的定义可得x+c=2a,
∴x=2a﹣c
过点![]() 作x轴的垂线,点P到该垂线的距离为2a
作x轴的垂线,点P到该垂线的距离为2a
由勾股定理 y2+4a2=4b2,即4c(2a﹣c)+4a2=4(c2﹣a2)
得e2﹣e﹣1=0,
∴e=![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形,  面
面 ,
,  为
为 的中点。
的中点。(1)证明:
 平面
平面 ;
;(2)设
 ,
,  ,三棱锥
,三棱锥 的体积
的体积 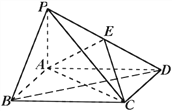 ,求A到平面PBC的距离。
,求A到平面PBC的距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数,
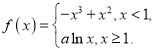
(1)求
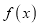 在区间
在区间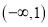 上的极小值和极大值;
上的极小值和极大值;(2)求
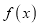 在
在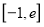 (
(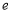 为自然对数的底数)上的最大值.
为自然对数的底数)上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
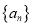 的前
的前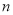 项和为
项和为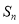 ,且对任意正整数
,且对任意正整数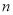 ,都有
,都有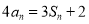 成立.记
成立.记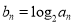 .
.(Ⅰ)求数列
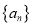 和
和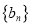 的通项公式;
的通项公式;(Ⅱ)设
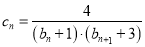 ,数列
,数列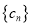 的前
的前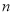 项和为
项和为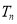 ,求证:
,求证: 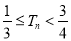 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润
 与时间
与时间 的关系,可选用
的关系,可选用A.一次函数B.二次函数
C.指数型函数D.对数型函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务的时间的统计数据如下表:
超过1小时
不超过1小时
男
20
8
女
12
m
(1)求m,n;
(2)能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
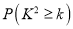
0.050
0.010
0.001
k
3.841
6.635
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查中学生每天玩游戏的时间是否与性别有关,随机抽取了男、女学生各50人进行调查,根据其日均玩游戏的时间绘制了如下的频率分布直方图.

(1)求所调查学生日均玩游戏时间在
 分钟的人数;
分钟的人数;(2)将日均玩游戏时间不低于60分钟的学生称为“游戏迷”,已知“游戏迷”中女生有6人;根据已知条件,完成下面的
 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;非游戏迷
游戏迷
合计
男
女
合计
附:
 (其中
(其中 为样本容量).
为样本容量).
0.15
0.10
0.05
0.025
0.010

2.072
2.706
3.841
5.024
6.635
相关试题

