【题目】为了调查中学生每天玩游戏的时间是否与性别有关,随机抽取了男、女学生各50人进行调查,根据其日均玩游戏的时间绘制了如下的频率分布直方图.

(1)求所调查学生日均玩游戏时间在![]() 分钟的人数;
分钟的人数;
(2)将日均玩游戏时间不低于60分钟的学生称为“游戏迷”,已知“游戏迷”中女生有6人;根据已知条件,完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
非游戏迷 | 游戏迷 | 合计 | |
男 | |||
女 | |||
合计 |
附: (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考答案:
【答案】(1)![]() 人(2)填表见解析,能在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别有关
人(2)填表见解析,能在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别有关
【解析】
(1)根据频率分布直方图得到每段的频率,利用频率之和等于1,得到在![]() 分钟的频率,从而得到所求的人数;(2)根据“游戏迷”的频率得到“游戏迷”的人数,根据“游戏迷”女生人数,求出“游戏迷”男生人数,填写列联表,根据公式计算出
分钟的频率,从而得到所求的人数;(2)根据“游戏迷”的频率得到“游戏迷”的人数,根据“游戏迷”女生人数,求出“游戏迷”男生人数,填写列联表,根据公式计算出![]() ,然后得到结论.
,然后得到结论.
(1).日均玩游戏时间在![]() 分钟的频率为
分钟的频率为![]() ,
,
所以,所调查学生日均玩游戏时间在![]() 分钟的人数为
分钟的人数为![]() .
.
(2).“游戏迷”的频率为![]() ,
,
共有“游戏迷”![]() 人,由于“游戏迷”中女生有6人,故男生有14人.
人,由于“游戏迷”中女生有6人,故男生有14人.
根据男、女学生各有50人,得列联表如下:
非游戏迷 | 游戏迷 | 合计 | |
男 | 36 | 14 | 50 |
女 | 44 | 6 | 50 |
合计 | 80 | 20 | 100 |
![]() .
.
故能在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过双曲线
 的左焦点
的左焦点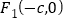 作圆
作圆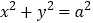 的切线,切点为
的切线,切点为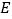 ,延长
,延长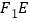 交抛物线
交抛物线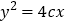 于点
于点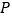 ,若
,若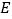 是线段
是线段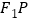 的中点,则双曲线的离心率是( )
的中点,则双曲线的离心率是( )A.
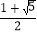 B.
B. 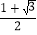 C.
C. 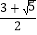 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润
 与时间
与时间 的关系,可选用
的关系,可选用A.一次函数B.二次函数
C.指数型函数D.对数型函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务的时间的统计数据如下表:
超过1小时
不超过1小时
男
20
8
女
12
m
(1)求m,n;
(2)能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
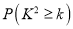
0.050
0.010
0.001
k
3.841
6.635
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实国务院“提速降费”的要求,某市移动公司欲下调移动用户消费资费.已知该公司共有移动用户10万人,人均月消费50元.经测算,若人均月消费下降x%,则用户人数会增加
 万人.
万人.(1)若要保证该公司月总收入不减少,试求x的取值范围;
(2)为了布局“5G网络”,该公司拟定投入资金进行5G网络基站建设,投入资金方式为每位用户月消费中固定划出2元进入基站建设资金,若使该公司总盈利最大,试求x的值.
(总盈利资金=总收入资金-总投入资金)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.规定:每辆自行车的日租金不超过20元,每辆自行车的日租金
 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用
元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用 表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).
表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).(1)求函数
 的解析式及定义域;
的解析式及定义域;(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
相关试题

