【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
参考答案:
【答案】③⑤
【解析】对于①,![]() 时,
时, ![]() ,而
,而![]() ,故①错误;对于②,
,故①错误;对于②,![]() 在
在![]() 上递增,故②错误;对于③,
上递增,故②错误;对于③,![]() 时,
时, ![]() ,
, ![]() 是
是![]() 的对称轴,故③正确;对于④,
的对称轴,故③正确;对于④,![]() 时,
时, ![]() 不是
不是![]() 的对称中心,故④错误;对于⑤,
的对称中心,故④错误;对于⑤,![]() ,设
,设![]() 因为
因为![]() ,所以
,所以![]() ,则
,则![]() ,
, ![]() 在
在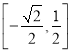 上递增,在
上递增,在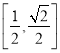 上递减,因为
上递减,因为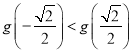 可得
可得![]() 时,
时, ![]() ,即函数
,即函数![]() 的最小值是
的最小值是![]() ,故⑤正确,故答案为③⑤.
,故⑤正确,故答案为③⑤.
【 方法点睛】本题主要通过对多个命题真假的判断,综合考查三角函数的单调性、三角函数的奇偶性、三角函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 的半径为2,圆心在
的半径为2,圆心在 轴的正半轴上,且与直线
轴的正半轴上,且与直线 相切.
相切.(1)求圆
 的方程。
的方程。(2)在圆
 上,是否存在点
上,是否存在点 ,使得直线
,使得直线 与圆
与圆 相交于不同的两点
相交于不同的两点 ,且△
,且△ 的面积最大?若存在,求出点
的面积最大?若存在,求出点 的坐标及对应的△
的坐标及对应的△ 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份
2010
2011
2012
2013
2014
2015
2016
年份代号x
1
2
3
4
5
6
7
人均纯收入y
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: =
=  ,
,  =
=  ﹣
﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|﹣|2x+1|的最大值为m
(1)作函数f(x)的图象
(2)若a2+b2+2c2=m,求ab+2bc的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注
关注
总计
男生
30
15
45
女生
45
10
55
总计
75
25
100
根据表中数据,通过计算统计量K2=
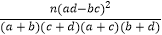 ,并参考一下临界数据:
,并参考一下临界数据:P(K2>k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( )的最大值为
)的最大值为 ,最小值为
,最小值为 .
.(1)求
 的值;
的值;(2)将函数
 图象向右平移
图象向右平移 个单位后,再将图象上所有点的纵坐标扩大到原来的
个单位后,再将图象上所有点的纵坐标扩大到原来的 倍,横坐标不变,得到函数
倍,横坐标不变,得到函数 的图象,求方程
的图象,求方程 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
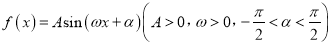 的最小正周期为
的最小正周期为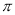 ,且当
,且当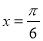 时,
时, 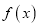 取得最大值
取得最大值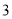 .
.(1)求
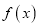 的解析式及单调增区间;
的解析式及单调增区间;(2)若
 ,且
,且 ,求
,求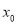 ;
;(3)将函数
 的图象向右平移
的图象向右平移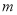 (
(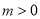 )个单位长度后得到函数
)个单位长度后得到函数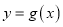 是偶函数,求
是偶函数,求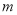 的最小值.
的最小值.
相关试题

