【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() . (2)见解析.
. (2)见解析.
【解析】试题分析:(1)设圆心是![]() ,由直线
,由直线![]() 于圆相切可知,圆心到直线的距离等于半径,利用点到直线的距离公式可求
于圆相切可知,圆心到直线的距离等于半径,利用点到直线的距离公式可求![]() ,进而可求圆
,进而可求圆![]() 的方程;(2)把点
的方程;(2)把点![]() 代入圆的方程可得,
代入圆的方程可得, ![]() 的方程,结合原点到直线
的方程,结合原点到直线![]() 的距离
的距离![]() ,可求
,可求![]() 的范围,根据弦长公式求出
的范围,根据弦长公式求出![]() ,代入三角形的面积公式,结合二次函数的性质可求最大值.
,代入三角形的面积公式,结合二次函数的性质可求最大值.
试题解析:(1)设圆心是![]() ,它到直线
,它到直线![]() 的距离是
的距离是![]() ,解得
,解得
![]() 或
或![]() (舍去),
(舍去),
所以所求圆![]() 的方程是
的方程是![]() .
.
(2)存在,理由如下:因为点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,
![]() 且
且![]() .
.
又因为原点到直线![]() 的距离
的距离![]() ,
,
解得![]() ,而
,而![]() ,
,
所以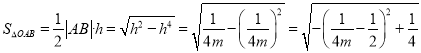 ,
,
因为![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,
,
此时点![]() 的坐标是
的坐标是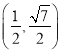 或
或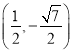 ,
, ![]() 的面积的最大值是
的面积的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据平面向量基本定理,若
 为一组基底,同一平面的向量
为一组基底,同一平面的向量 可以被唯一确定地表示为
可以被唯一确定地表示为  =
=  ,则向量
,则向量 与有序实数对
与有序实数对 一一对应,称
一一对应,称 为向量
为向量 的基底
的基底 下的坐标;特别地,若
下的坐标;特别地,若 分别为
分别为 轴正方向的单位向量
轴正方向的单位向量 ,则称
,则称 为向量
为向量 的直角坐标.
的直角坐标.(I)据此证明向量加法的直角坐标公式:若
 ,则
,则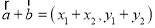 ;
;(II)如图,直角
 中,
中,  ,
,  点在
点在 上,且
上,且 ,求向量
,求向量 在基底
在基底 下的坐标.
下的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
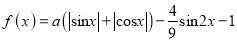 ,若
,若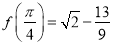
(1)求
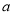 的值,并写出函数
的值,并写出函数 的最小正周期(不需证明);
的最小正周期(不需证明);(2)是否存在正整数
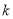 ,使得函数
,使得函数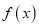 在区间
在区间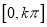 内恰有
内恰有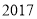 个零点?若存在,求出
个零点?若存在,求出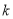 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn=
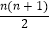 ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份
2010
2011
2012
2013
2014
2015
2016
年份代号x
1
2
3
4
5
6
7
人均纯收入y
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: =
=  ,
,  =
=  ﹣
﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|﹣|2x+1|的最大值为m
(1)作函数f(x)的图象
(2)若a2+b2+2c2=m,求ab+2bc的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①若
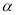 ,
,  是第一象限角且
是第一象限角且 ,则
,则 ;
;②函数
 在
在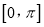 上是减函数;
上是减函数;③
 是函数
是函数 的一条对称轴;
的一条对称轴;④函数
 的图象关于点
的图象关于点 成中心对称;
成中心对称;⑤设
 ,则函数
,则函数 的最小值是
的最小值是 ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
相关试题

