搜索
【题目】若函数f（x）是偶函数，且在（﹣∞，0]上是增函数，又f（2）=0，则xf（x）＞0的解集是（ ）
A.（﹣2，2）
B.（﹣∞，﹣2）∪（0，2）
C.（﹣∞，﹣2）∪（2，+∞）
D.（﹣2，0]∪（2，+∞）
参考答案：
【答案】B
【解析】解：∵偶函数f（x）在（﹣∞，0]上为增函数，又f（﹣2）=0，
∴函数f（x）在（0，+∞）上为减函数，且f（﹣2）=f（2）=0，
画出函数f（x）的示意图如图所示：
∵不等式xf（x）＞0等价为 
或 
，
∴由图得，0＜x＜2或x＜﹣2，
∴不等式的解集是（﹣∞，﹣2）∪（0，2），
故选：B．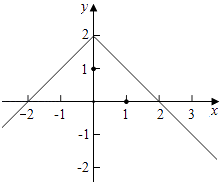
【考点精析】认真审题，首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若函数y=f（x）的定义域是[0，4]，则函数g（x）=
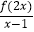的定义域是（ ）
A.[0，2]
B.[0，2）
C.[0，1）∪（1，2]
D.[0，4] -
科目： 来源： 题型：
查看答案和解析>>【题目】为调查了解某省属师范大学师范类毕业生参加工作后，从事的工作与教育是否有关的情况，该校随机调查了该校80位性别不同的2016年师范类毕业大学生，得到具体数据如下表：
与教育有关
与教育无关
合计
男
30
10
40
女
35
5
40
合计
65
15
80
（1）能否在犯错误的概率不超过5%的前提下，认为“师范类毕业生从事与教育有关的工作与性别有关”？
参考公式：
（
）．附表：
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.455
0.708
1.323
2.072
2.706
3.841
5.023
6.635
（2）求这80位师范类毕业生从事与教育有关工作的频率；
（3）以（2）中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名，记这4名毕业生从事与教育有关的人数为
，求
的数学期望
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数f（x）的最小值为1，且f（0）=f（2）=3．
（1）求f（x）的解析式；
（2）若f（x）在区间[2a，a+1]上不单调，求实数a的取值范围；
（3）在区间[﹣1，1]上，y=f（x）的图象恒在y=2x+2m+1的图象上方，试确定实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】若A={x|2x≤（
）x﹣2}，则函数y=（ 
）x（x∈A）的值域为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分12分）设函数
．（Ⅰ）若函数
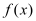在定义域上为增函数，求实数
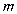的取值范围；（Ⅱ）在（Ⅰ）的条件下，若函数
，
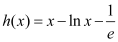使得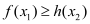
成立，求实数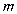的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某种大型商品，A，B两地都有出售，且价格相同、某地居民从两地之一购得商品后运回的费用是：每单位距离A地的运费是B地的运费的3倍，已知A，B两地距离为10千米，顾客选择A或B地购买这种商品的标准是：包括运费和价格的总费用较低，求A，B两地的售货区域的分界线的曲线形状，并指出曲线上、曲线内、曲线外的居民应如何选择购货地点
相关试题
