【题目】已知函数f(x)=x﹣alnx,(a∈R).
(1)讨论函数f(x)在定义域内的极值点的个数;
(2)设g(x)=﹣ ![]() ,若不等式f(x)>g(x)对任意x∈[1,e]恒成立,求a的取值范围.
,若不等式f(x)>g(x)对任意x∈[1,e]恒成立,求a的取值范围.
参考答案:
【答案】
(1)解:f(x)=x﹣alnx,(x>0),
f′(x)=1﹣ ![]() =
= ![]() ,
,
①a≤0时,f′(x)>0,f(x)递增,f(x)无极值;
②a>0时,令f′(x)>0,解得:x>a,令f′(x)<0,解得:0<x<a,
∴f(x)在(0,a)递减,在(a,+∞)递增,
f(x)有1个极小值点;
(2)解:若不等式f(x)>g(x)对任意x∈[1,e]恒成立,
令h(x)=f(x)﹣g(x),即h(x)最小值>0在[1,e]恒成立,
则h(x)=x﹣alnx+ ![]() (a∈R),
(a∈R),
∴h′(x)=1﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
①当1+a≤0,即a≤﹣1时,在[1,e]上为增函数,f(x)min=f(1)=1+1+a>0,
解得:a>﹣2,即﹣2<a≤﹣1,
当a>﹣1时
①当1+a≥e时,即a≥e﹣1时,f(x)在[1,e]上单调递减,
∴f(x)min=f(e)=e+ ![]() ﹣a>0,解得a<
﹣a>0,解得a< ![]() ,
,
∵ ![]() >e﹣1,
>e﹣1,
∴e﹣1≤a< ![]() ;
;
②当0<1+a≤1,即﹣1<a≤0,f(x)在[1,e]上单调递增,
∴f(x)min=f(1)=1+1+a>0,
解得a>﹣2,故﹣2<a<﹣1;
③当1<1+a<e,即0<a<e﹣1时,f(x)min=f(1+a),
∵0<ln(1+a)<1,
∴0<aln(1+a)<a,
∴f(1+a)=a+2﹣aln(1+a)>2,此时f(1+a)>0成立,
综上,﹣2<a< ![]() 时,不等式f(x)>g(x)对任意x∈[1,e]恒成立
时,不等式f(x)>g(x)对任意x∈[1,e]恒成立
【解析】(1)先求导,再分类讨论,得到函数的单调区间,从而求出函数的极值点的个数;(2)由题意,只要求出函数f(x)min>0即可,利用导数和函数的最值的关系,进行分类讨论,即可得到a的范围.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值),还要掌握函数的最大(小)值与导数(求函数
是极小值),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=2,解不等式f(x)≥2;
(2)已知f(x)是偶函数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
 (b2+c2﹣a2),则∠B=( )
(b2+c2﹣a2),则∠B=( )
A.90°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的奇函数f(x),当x>0时,f(x)=x﹣2
(1)求函数f(x)的解析式;
(2)求不等式f(x)<2的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=
 x3+bx2+(b+2)x+3是R上的单调增函数,则b的取值是( )
x3+bx2+(b+2)x+3是R上的单调增函数,则b的取值是( )
A.b<﹣1或b>2
B.b≤﹣2或b≥2
C.﹣1<b<2
D.﹣1≤b≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 :
: 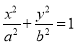 ,其左右焦点为
,其左右焦点为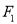
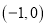 及
及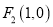 ,过点
,过点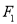 的直线交椭圆
的直线交椭圆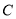 于
于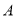 ,
,  两点,线段
两点,线段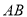 的中点为
的中点为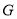 ,
, 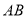 的中垂线与
的中垂线与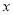 轴和
轴和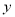 轴分别交于
轴分别交于 ,
, 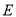 两点,且
两点,且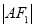 、
、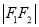 、
、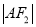 构成等差数列.
构成等差数列.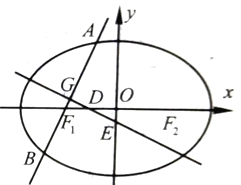
(1)求椭圆
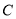 的方程;
的方程;(2)记
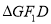 的面积为
的面积为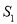 ,
, 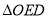 (
(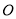 为原点)的面积为
为原点)的面积为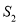 .试问:是否存在直线
.试问:是否存在直线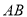 ,使得
,使得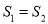 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
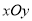 中,圆
中,圆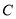 的方程为
的方程为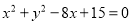 ,若直线
,若直线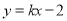 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆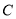 有公共点,则
有公共点,则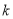 的最大值为__________.
的最大值为__________.
相关试题

