【题目】已知 ![]() 是定义在(﹣∞,+∞)上的奇函数,且满足
是定义在(﹣∞,+∞)上的奇函数,且满足 ![]()
(1)求实数a,b,并确定函数f(x)的解析式
(2)用定义证明f(x)在(﹣1,1)上是增函数.
参考答案:
【答案】
(1)解:由满足 ![]() ,
,
∴ 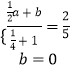 ,解得
,解得 ![]() .
.
∴a=1,b=0, ![]()
(2)证明:设﹣1<x1<x2<1,
![]() =
= ![]() ,
,
∵﹣1<x1<x2<﹣1,∴﹣1<x1x2<1,即1﹣x1x2>0,x2﹣x1>0, ![]() ,
, ![]() ,
,
∴f(x2)﹣f(x1)>0,即f(x2)>f(x1).
所以函数f(x)在(﹣1,1)上是增函数
【解析】(1)利用函数的奇偶性即可求出;(2)利用函数的单调性即可证明.
【考点精析】利用函数单调性的判断方法对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
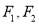 分别为椭圆
分别为椭圆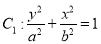 的上、下焦点,
的上、下焦点, 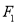 是抛物线
是抛物线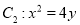 的焦点,点
的焦点,点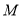 是
是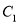 与
与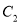 在第二象限的交点,且
在第二象限的交点,且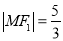 .
.(1)求椭圆
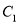 的方程;
的方程;(2)与圆
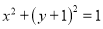 相切的直线
相切的直线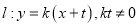 交椭圆
交椭圆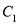 于
于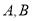 ,
,若椭圆
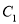 上一点
上一点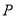 满足
满足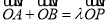 ,求实数
,求实数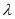 的取值范围.
的取值范围.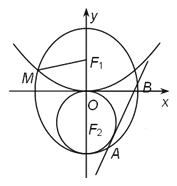
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
1)已知两平面的法向量分别为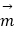 =(0,1,0),
=(0,1,0), 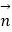 =(0,1,1),则两平面所成的二面角为45°或135°;
=(0,1,1),则两平面所成的二面角为45°或135°;
2)若曲线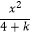 +
+ 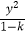 =1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
=1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
3)已知双曲线方程为x2﹣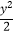 =1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
=1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
其中正确命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设F(x)=f(x)+f(﹣x)在区间
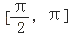 是单调递减函数,将F(x)的图象按向量
是单调递减函数,将F(x)的图象按向量 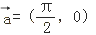 平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
A.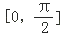
B.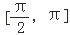
C.
D.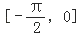
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=﹣2x+1且f(2)=15.
(1)求函数f(x)的解析式;
(2)令g(x)=(2﹣2m)x﹣f(x);
①若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
②求函数g(x)在x∈[0,2]的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=2sin(
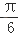 ﹣2x),x∈[0,π])为增函数的区间是( )
﹣2x),x∈[0,π])为增函数的区间是( )
A.[0,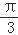 ]
]
B.[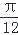 ,
, 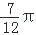 ]
]
C.[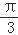 ,
,  ]
]
D.[ ,π]
,π] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线C1:
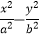 =1,(a>0,b>0)的焦距是实轴长的2倍,若抛物线C2:x2=2py,(p>0)的焦点到双曲线C1的渐近线的距离为2,求抛物线C2的标准方程.
=1,(a>0,b>0)的焦距是实轴长的2倍,若抛物线C2:x2=2py,(p>0)的焦点到双曲线C1的渐近线的距离为2,求抛物线C2的标准方程.
相关试题

