【题目】用长为![]() ,宽为
,宽为![]() 的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转![]() ,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?

参考答案:
【答案】当容器高为10cm时,最大容积是19600cm2
【解析】试题分析:首先分析题目求长为90cm,宽为48cm的长方形铁皮做一个无盖的容器当容器的高为多少时,容器的容积最大.故可设容器的高为x,体积为V,求出v关于x的方程,然后求出导函数,分析单调性即可求得最值.
解:根据题意可设容器的高为x,容器的体积为V,
则有V=(90﹣2x)(48﹣2x)x=4x3﹣276x2+4320x,(0<x<24)
求导可得到:V′=12x2﹣552x+4320
由V′=12x2﹣552x+4320=0得x1=10,x2=36.
所以当x<10时,V′>0,
当10<x<36时,V′<0,
当x>36时,V′>0,
所以,当x=10,V有极大值V(10)=19600,又V(0)=0,V(24)=0,
所以当x=10,V有最大值V(10)=19600
故答案为当高为10,最大容积为19600.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
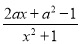 ,其中a∈R.
,其中a∈R. (I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心为原点,且与直线
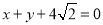 相切.
相切.(1)求圆C的方程;
(2)点
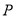 在直线
在直线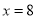 上,过
上,过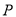 点引圆C的两条切线
点引圆C的两条切线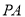 ,
, 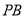 ,切点为
,切点为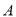 ,
, 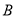 ,求证:直线
,求证:直线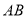 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=
 的a的值,并求此时函数的最大值.
的a的值,并求此时函数的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在实数a,使得函数y=sin2x+acosx+
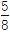 a-
a-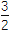 在闭区间[0,
在闭区间[0,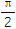 ]上的最大值是1?若存在,则求出对应的a的值;若不存在,则说明理由.
]上的最大值是1?若存在,则求出对应的a的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是解决数学问题的思维过程的流程图:
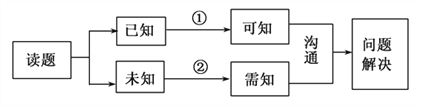
在此流程图中,①、②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.
 ①—分析法,②—反证法 B. ①—分析法,②—综合法
①—分析法,②—反证法 B. ①—分析法,②—综合法C. ①—综合法,②—反证法 D. ①—综合法,②—分析法
相关试题

