【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
参考答案:
【答案】(I)![]() ; (II)b<-
; (II)b<-![]()
【解析】试题分析:(1)首先对f(x)求导,然后由题设在x=1时有极值10可得f '(1)=0,f(1)=10,解得即可;
(2)x3-x2+bx+1<0在x∈[1,2]恒成立,即b<![]() 在x∈[1,2]恒成立,令g(x)=
在x∈[1,2]恒成立,令g(x)=![]() ,即可求出b的取值范围.
,即可求出b的取值范围.
试题解析:
(I)f '(x)=3x2+2ax+b,由题设有f '(1)=0,f(1)=10
即![]() 解得
解得![]() 或
或![]()
经验证,若![]() 则f '(x)=3x2-6x+3=3(x-1)2
则f '(x)=3x2-6x+3=3(x-1)2
当x>1或x<1时,均有f '(x)>0,可知
此时x=1不是f(x)的极值点,故![]() 舍去
舍去
![]() 符合题意,故
符合题意,故![]() .
.
(II)当a=-1时,f(x)=x3-x2+bx+l
若f(x)<0在x∈[1,2]恒成立,即
x3-x2+bx+1<0在x∈[1,2]恒成立
即b<![]() 在x∈[1,2]恒成立
在x∈[1,2]恒成立
令g(x)=![]() ,则
,则
g '(x)=![]() =
=![]()
(法一:由g '(x)=0解得x=1…)
(法二)由-2x3+x2+1=1-x3+x2(1-x) 可知x∈[1,2]时g '(x)<0
即g(x)=![]() 在x∈[1,2]单调递减
在x∈[1,2]单调递减
(g(x))max=g(2)=-![]()
∴b<-![]() 时,f(x)<0在x∈[1,2]恒成立.
时,f(x)<0在x∈[1,2]恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区工商局、消费者协会在
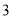 月
月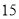 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取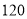 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第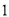 组
组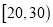 ,第
,第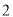 组
组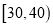 ,第
,第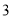 组
组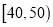 ,第
,第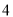 组
组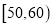 ,第
,第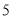 组
组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.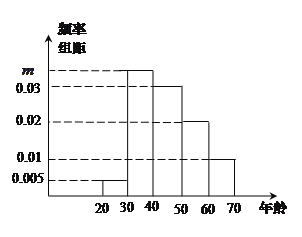
(Ⅰ)若电视台记者要从抽取的群众中选
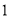 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第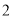 组或第
组或第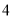 组的概率;
组的概率;(Ⅱ)已知第
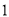 组群众中男性有
组群众中男性有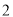 人,组织方要从第
人,组织方要从第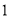 组中随机抽取
组中随机抽取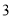 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形,  平面
平面 ,
,  ,点
,点 为
为 的中点,点
的中点,点 在棱
在棱 上移动.
上移动.(1)当点
 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求证:无论点
 在
在 的何处,都有
的何处,都有 ;
;(3)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
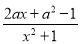 ,其中a∈R.
,其中a∈R. (I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数①f(x)=4x+
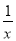 -5,②f(x)=|log2 x|-(
-5,②f(x)=|log2 x|-(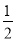 )x,③f(x)=cos(x+2)-cosx,判断如下两个命题的真假:
)x,③f(x)=cos(x+2)-cosx,判断如下两个命题的真假:命题甲:f(x)在区间(1,2)上是增函数;
命题乙:f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.
能使命题甲、乙均为真的函数的序号是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3-3ax+e,g(x)=1-lnx,其中e为自然对数的底数.
(I)若曲线y=f(x)在点(1,f(1))处的切线与直线l:x+2y=0垂直,求实数a的值;
(II)设函数F(x)=-x[g(x)+
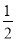 x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;
x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;(III)用max{m,n}表示m,n中的较大者,记函数h(x)=max{f(x),g(x)}(x>0). 若函数h(x)在(0,+∞)上恰有2个零点,求实数a的取值范围.
相关试题

