【题目】已知函数f(x)=![]() ,其中a∈R.
,其中a∈R.
(I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
参考答案:
【答案】(I)2x-y=0; (II)见解析.
【解析】试题分析:(1)求出在原点处的导数值,得斜率,即可求出切线方程;
(2)求出导数,讨论单调性得极值.
试题解析:
(I)解:当a=1时,f(x)=![]() ,f '(x)=-2
,f '(x)=-2 .…………2分
.…………2分
由f '(0)=2,得曲线y=f(x)在原点处的切线方程是2x-y=0.………4分
(II)解:f '(x)=-2![]() . ………6分
. ………6分
①当a=0时,f '(x)=![]() .
.
所以f(x)在(0,+∞)单调递增,(-∞,0)单调递减. ………………7分
当a≠0,f '(x)=-2a .
.
②当a>0时,令f '(x)=0,得x1=-a,x2=![]() ,f(x)与f '(x)的情况如下:
,f(x)与f '(x)的情况如下:
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f '(x) | - | 0 | + | 0 | - |
f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
故f(x)的单调减区间是(-∞,-a),(![]() ,+∞);单调增区间是(-a,
,+∞);单调增区间是(-a, ![]() ).
).
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………10分
)=a2 ………10分
③当a<0时,f(x)与f '(x)的情况如下:
x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
f '(x) | + | 0 | - | 0 | + |
f(x) | ↗ | f(x2) | ↘ | f(x1) | ↗ |
所以f(x)的单调增区间是(-∞,![]() );单调减区间是(-
);单调减区间是(-![]() ,-a),(-a,+ ∞)。
,-a),(-a,+ ∞)。
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………………12分
)=a2 ………………12分
综上,a>0时,f(x)在(-∞,-a),(![]() ,+∞)单调递减;在(-a,
,+∞)单调递减;在(-a, ![]() )单调递增.
)单调递增.
a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减,f(x)有极小值f(-a)=-1,有极大值,f(![]() )=a2;a<0时,f(x)在(-∞,
)=a2;a<0时,f(x)在(-∞, ![]() ),(-a,+∞)单调递增;在(
),(-a,+∞)单调递增;在(![]() ,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(
,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2.
)=a2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=elnx,g(x)=
 f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)(1)求函数g(x)的极大值;
(2)求证:1+
 +
+ +…+
+…+ >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)y=
 的单调递减区间是_____________.
的单调递减区间是_____________.(2)y=
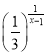 的递增区间是____________________
的递增区间是____________________ -
科目: 来源: 题型:
查看答案和解析>>【题目】设P、Q为两个非空集合,定义集合P+Q={m+n| m∈P,n∈Q},若P={0,2,5}, Q={1,2,6},则P+Q中元素的个数为 ( )
A. 9 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心为原点,且与直线
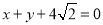 相切.
相切.(1)求圆C的方程;
(2)点
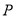 在直线
在直线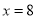 上,过
上,过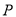 点引圆C的两条切线
点引圆C的两条切线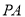 ,
, 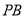 ,切点为
,切点为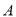 ,
, 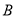 ,求证:直线
,求证:直线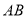 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=
 的a的值,并求此时函数的最大值.
的a的值,并求此时函数的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用长为
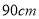 ,宽为
,宽为 的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转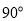 ,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
相关试题

