【题目】已知函数![]() 在点
在点![]() 处的切线是
处的切线是![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 恒成立时,求实数
恒成立时,求实数![]() 的取值范围(
的取值范围(![]() 为自然对数的底数).
为自然对数的底数).
参考答案:
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意可得函数的解析式![]() (
(![]() ),则
),则![]() ,
,![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)原问题等价于![]() 在
在![]() 恒成立,
恒成立,
【法一】设![]() ,由题意可得
,由题意可得![]() ;
;![]() .据此有
.据此有![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
【法二】设![]() (
(![]() ),则
),则![]() ,
,
结合导函数的解析式可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.所以
上单调递减.所以![]() ,即
,即![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)因为![]() ,所以
,所以![]() ,
,
因为点![]() 处的切线是
处的切线是![]() ,所以
,所以![]() ,且
,且![]()
所以![]() ,即
,即![]() (
(![]() )
)
所以![]() ,所以在
,所以在![]() 上递增,在
上递增,在![]() 上递减
上递减
所以![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)当![]() 在
在![]() 恒成立时,由(1)
恒成立时,由(1)![]() ,
,
即![]() 在
在![]() 恒成立,
恒成立,
【法一】设![]() ,则
,则![]() ,
,![]() ,
,
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() ;
;
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() .
.
所以![]() 均在
均在![]() 处取得最值,所以要使
处取得最值,所以要使![]() 恒成立,
恒成立,
只需![]() ,即
,即![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
【法二】设![]() (
(![]() ),则
),则![]()
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,
,![]() ,即
,即![]()
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,
,![]() ,即
,即![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() ,即
,即![]() ,又
,又![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三棱柱
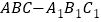 的所有棱长均
的所有棱长均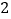 ,
,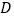 为棱
为棱 (不包括端点)上一动点,
(不包括端点)上一动点,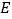 是
是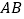 的中点.
的中点.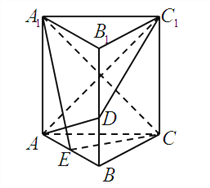
(Ⅰ)若
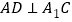 ,求
,求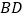 的长;
的长;(Ⅱ)当
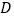 在棱
在棱 (不包括端点)上运动时,求平面
(不包括端点)上运动时,求平面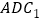 与平面
与平面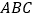 的夹角的余弦值的取值范围.
的夹角的余弦值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】最近,“百万英雄”,“冲顶大会”等一些闯关答题类游戏风靡全国,既能答题,又能学知识,还能挣奖金。若某闯关答题一轮共有4类题型,选手从前往后逐类回答,若中途回答错误,立马淘汰只能观战;若能坚持到4类题型全部回答正确,就能分得现金并获得一枚复活币。每一轮闯关答题顺序为:1.文史常识类;2.数理常识类;3.生活常识类;4.影视艺术常识类,现从全省高中生中调查了100位同学的答题情况统计如下表:

(Ⅰ)现用样本的数据特征估算整体的数据特征,从全省高中生挑选4位同学,记
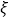 为4位同学获得奖金的总人数,求
为4位同学获得奖金的总人数,求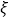 的分布列和期望.
的分布列和期望.(Ⅱ)若王同学某轮闯关获得的复活币,系统会在下一轮游戏中自动使用,即下一轮重新进行闯关答题时,若王同学在某一类题型中回答错误,自动复活一次,视为答对该类题型。请问:仍用样本的数据特征估算王同学的数据特征,那么王同学在获得复活币的下一轮答题游戏中能够最终获得奖金的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
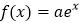 ,
,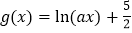 ,
, .
.(Ⅰ)若
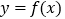 的图像在
的图像在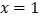 处的切线过点
处的切线过点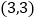 ,求
,求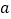 的值并讨论
的值并讨论 在
在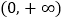 上的单调增区间;
上的单调增区间;(Ⅱ)定义:若直线
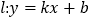 与曲线
与曲线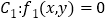 、
、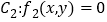 都相切,则我们称直线
都相切,则我们称直线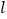 为曲线
为曲线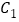 、
、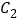 的公切线.若曲线
的公切线.若曲线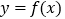 与
与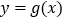 存在公切线,试求实数
存在公切线,试求实数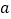 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
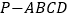 中,
中,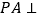 底面
底面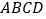 ,
,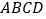 为直角梯形,
为直角梯形,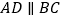 ,
,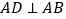 ,
,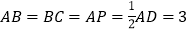 ,
,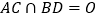 ,过
,过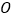 点作平面
点作平面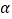 平行于平面
平行于平面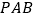 ,平面
,平面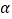 与棱
与棱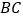 ,
,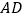 ,
,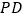 ,
,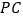 分别相交于点
分别相交于点 ,
,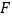 ,
,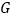 ,
,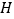 .
.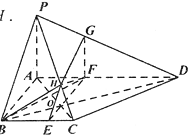
(1)求
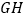 的长度;
的长度;(2)求二面角
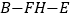 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在
 ,按照区间
,按照区间 ,
, ,
, ,
, ,
, 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
完成表格,并判断是否有
 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
(2)从乙班
 ,
, ,
, 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自 发言的人数为随机变量
发言的人数为随机变量 ,求
,求 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数再取整,绘制成如下茎叶图,规定不低于85分(百分制)为优秀,甲班同学成绩的中位数为74.


(1)求
 的值和乙班同学成绩的众数;
的值和乙班同学成绩的众数;(2)完成表格,若有
 以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
相关试题

