【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.

完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;

(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:
(1)依题意得![]() ,则有90%以上的把握认为“数学成绩优秀与教学改革有关”.
,则有90%以上的把握认为“数学成绩优秀与教学改革有关”.
(2)由题意可得随机变量![]() 的所有可能取值为
的所有可能取值为![]() 且
且![]() ,据此可得分布列,计算数学期望
,据此可得分布列,计算数学期望![]() .
.
试题解析:
(1)依题意得![]()

有90%以上的把握认为“数学成绩优秀与教学改革有关”
(2)从乙班![]() 分数段中抽人数分别为2,3,2
分数段中抽人数分别为2,3,2
依题意随机变量![]() 的所有可能取值为
的所有可能取值为![]()
 ,
,
则分布列:
|
|
|
|
|
|
|
|
|
|
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
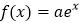 ,
,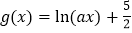 ,
, .
.(Ⅰ)若
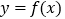 的图像在
的图像在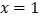 处的切线过点
处的切线过点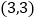 ,求
,求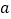 的值并讨论
的值并讨论 在
在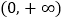 上的单调增区间;
上的单调增区间;(Ⅱ)定义:若直线
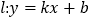 与曲线
与曲线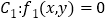 、
、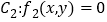 都相切,则我们称直线
都相切,则我们称直线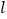 为曲线
为曲线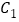 、
、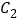 的公切线.若曲线
的公切线.若曲线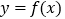 与
与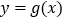 存在公切线,试求实数
存在公切线,试求实数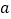 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
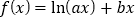 在点
在点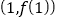 处的切线是
处的切线是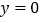 .
.(1)求函数
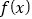 的极值;
的极值;(2)当
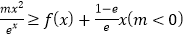 恒成立时,求实数
恒成立时,求实数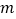 的取值范围(
的取值范围(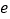 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
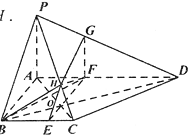
查看答案和解析>>【题目】如图,四棱锥
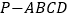 中,
中,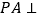 底面
底面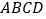 ,
,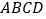 为直角梯形,
为直角梯形,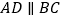 ,
,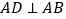 ,
,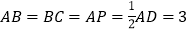 ,
,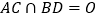 ,过
,过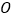 点作平面
点作平面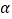 平行于平面
平行于平面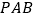 ,平面
,平面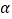 与棱
与棱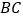 ,
,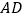 ,
,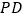 ,
,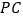 分别相交于点
分别相交于点 ,
,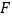 ,
,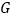 ,
,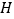 .
.
(1)求
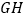 的长度;
的长度;(2)求二面角
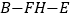 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数再取整,绘制成如下茎叶图,规定不低于85分(百分制)为优秀,甲班同学成绩的中位数为74.


(1)求
 的值和乙班同学成绩的众数;
的值和乙班同学成绩的众数;(2)完成表格,若有
 以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中, 底面
底面 ,
, 为直角梯形,
为直角梯形, 与
与 相交于点
相交于点 ,
, ,
, ,
, ,三棱锥
,三棱锥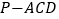 的体积为9.
的体积为9.
(1)求
 的值;
的值;(2)过
 点的平面
点的平面 平行于平面
平行于平面 ,
, 与棱
与棱 ,
, ,
, ,
, 分别相交于点
分别相交于点 ,求截面
,求截面 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的下顶点为
的下顶点为 ,右顶点为
,右顶点为 ,离心率
,离心率 ,抛物线
,抛物线 的焦点为
的焦点为 ,
, 是抛物线
是抛物线 上一点,抛物线
上一点,抛物线 在点
在点 处的切线为
处的切线为 ,且
,且 .
.(1)求直线
 的方程;
的方程;(2)若
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,且
两点,且 ,求
,求 的方程.
的方程.
相关试题

