【题目】如图所示,在正方体![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 的中点,
的中点,![]() 平面
平面![]()
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角
所成的角

参考答案:
【答案】(Ⅰ)见解析.(Ⅱ)![]() .
.
【解析】
(Ⅱ)利用正方体中的棱与面的关系可得CD⊥平面ADD1A1,进一步得到CD⊥AD1,再结合AD1⊥A1D,运用线面垂直的判定得答案;
(2)由已知MN⊥平面A1DC结合(1)的结论可得AD1与平面ABCD所成的角,就是MN与平面ABCD所成的角,进一步可得∠D1AD即为AD1与平面ABCD所成的角,则答案可求.
(Ⅰ)由![]() 是正方体知,
是正方体知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .又
.又![]() 为正方形,∴
为正方形,∴![]() .
.
 平面
平面![]() ;
;
(细则:先证![]() ,进而得出结论的也是6分)
,进而得出结论的也是6分)
(Ⅱ)∵![]() 平面
平面![]() ,又由(Ⅰ)知
,又由(Ⅰ)知![]() 平面
平面![]() ,∴
,∴![]()
∴![]() 与平面
与平面![]() 所成的角就是
所成的角就是![]() 与平面
与平面![]() 所成的角,
所成的角,
∵![]() 平面
平面![]() ,∴
,∴![]() 即为
即为![]() 与平面
与平面![]() 所成的角,
所成的角,
显然![]() ,∴
,∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
(细则:对于不同方法,只要正确的按对应步骤给分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,短轴长为
,短轴长为 .
.(1)求椭圆
 的方程;
的方程;(2)设
 ,
,  是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接 交椭圆
交椭圆 于另一点
于另一点 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;(3)在(2)的条件下,过点
 的直线与椭圆
的直线与椭圆 交于
交于 ,
,  两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.

(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知椭圆
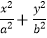 =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 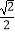 ,椭圆的右顶点为A.
,椭圆的右顶点为A.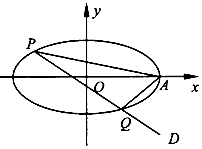
(1)求该椭圆的方程:
(2)过点D(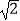 ,﹣
,﹣ 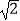 )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面,
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.
其中真命题的个数是( ).
A.
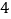 B.
B. 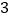 C.
C. 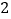 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱椎
 中,底面
中,底面 为菱形,
为菱形,  为
为 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)若
 底面
底面 ,
,  ,
,  ,
,  ,求三棱椎
,求三棱椎 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知梯形
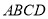 中,
中, 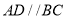 ,
, 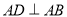 ,
, 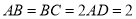 ,四边形
,四边形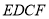 为矩形,
为矩形,  ,平面
,平面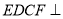 平面
平面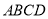 .
.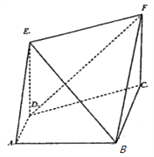
(Ⅰ)求证:
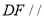 平面
平面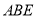 ;
;(Ⅱ)求平面
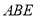 与平面
与平面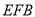 所成锐二面角的余弦值;
所成锐二面角的余弦值;(Ⅲ)在线段
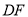 上是否存在点
上是否存在点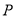 ,使得直线
,使得直线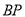 与平面
与平面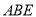 所成角的正弦值为
所成角的正弦值为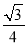 ,若存在,求出线段
,若存在,求出线段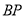 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
相关试题

