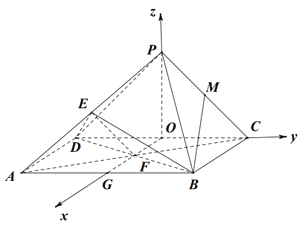
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(I)详见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】试题分析:
(1)利用题意证得![]() ,然后由线面平行的判断定理可得
,然后由线面平行的判断定理可得![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,利用平面向量的法向量可得二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)探索性问题,利用空间向量的结论可得在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
此时![]() .
.
试题解析:
(Ⅰ)证明:设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() .
.
因为![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,
在![]() 中,由已知
中,由已知![]() 为
为![]() 中点,
中点,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:取![]() 中点
中点![]() ,连接
,连接![]() .
.
因为![]() 是等腰三角形,
是等腰三角形, ![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
又因为平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
由题设知四边形![]() 为矩形,
为矩形,
所以![]() ,
,
所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则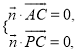 即
即![]()
令![]() ,则
,则![]() ,
, ![]() ,所以
,所以![]() .
.
平面![]() 的法向量为
的法向量为![]() ,
,
设![]() ,
, ![]() 的夹角为
的夹角为![]() ,所以
,所以![]() .
.
由图可知二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)设![]() 是棱
是棱![]() 上一点,则存在
上一点,则存在![]() 使得
使得![]() .
.
因此点![]() ,
, ![]() ,
, ![]() .
.
由![]() ,即
,即![]() .
.
因为![]() ,所以在棱
,所以在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
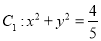 ,直线
,直线 与圆
与圆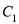 相切,且交椭圆
相切,且交椭圆 于
于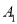 ,
, 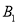 两点,
两点, 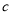 是椭圆的半焦距,
是椭圆的半焦距, 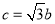 .
.(1)求
 的值;
的值;(2)
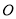 为坐标原点,若
为坐标原点,若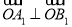 ,求椭圆
,求椭圆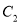 的方程;
的方程;(3)在(2)的条件下,设椭圆
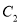 的左右顶点分别为
的左右顶点分别为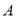 ,
,  ,动点
,动点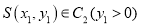 ,直线
,直线 ,
, 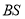 与直线
与直线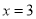 分别交于
分别交于 ,
, 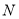 两点,求线段
两点,求线段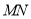 的长度的最小值.
的长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ﹣1
﹣1
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=|x|,g(x)=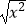
D.f(x)=1,g(x)=x0 -
科目: 来源: 题型:
查看答案和解析>>【题目】莫数学建模兴趣小组测量某移动信号塔
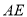 的高度
的高度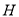 (单位:
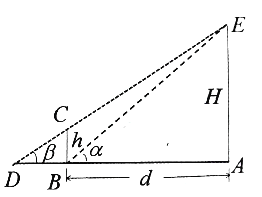
(单位: 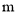 ),如图所示,垂直放置的标杆
),如图所示,垂直放置的标杆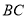 的高度
的高度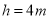 ,仰角
,仰角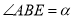 ,
, 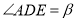 .
.
(Ⅰ)该小组已经测得一组
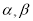 的值,
的值, 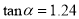 ,
, 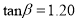 ,请推测
,请推测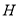 的值;
的值;(Ⅱ)该小组对测得的多组数据分析后,发现适当调节标杆到信号塔的距离
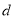 (单位:
(单位: 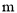 ),使得
),使得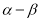 较大时,可以提高信号塔测量的精确度,若信号塔高度为
较大时,可以提高信号塔测量的精确度,若信号塔高度为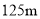 ,试问
,试问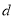 为多大时,
为多大时, 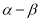 最大?
最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
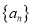 的前
的前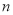 项和为
项和为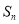 ,
,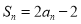 .
.(1)求数列
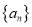 的通项公式;
的通项公式;(2)设
 ,
,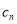 =
=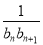 ,记数列
,记数列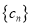 的前
的前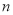 项和
项和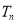 .若对
.若对 ,
, 恒成立,求实数
恒成立,求实数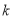 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①函数f(x)=( )x的递减区间是(﹣∞,+∞)
)x的递减区间是(﹣∞,+∞)
②已知函数f(x)的定义域为(0,1),则函数f(x+1)的定义域为(1,2);
③已知(x,y)映射f下的象是(x+y,x﹣y),那么(4,2)在f下的原象是(3,1).
其中正确命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计) 即为中奖.

乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
相关试题

