【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计) 即为中奖.

乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
参考答案:
【答案】在乙商场中奖的可能性大
【解析】试题分析:根据题意可知需分别求出在两个商场中奖的概率,然后比较中奖概率的大小即可知道结论.显然甲商场属于几何概型,需要求得阴影部分的面积占整个圆形面积的概率即为甲商场中奖的概率;乙商场中奖的概率根据古典概型,列出所有的基本事件数,进而得到中奖的事件数,进而求得乙商场中奖的概率,进而比较得到乙商场中奖的可能性大的结论.
试题解析:设顾客去甲商场,转动圆盘,指针指向阴影部分为事件![]() ,
,
试验的全部结果构成的区域为圆盘,面积为![]() (
(![]() 为圆盘的半径),阴影区域的面积为
为圆盘的半径),阴影区域的面积为![]() .
.
所以, 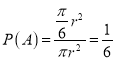 .
.
设顾客去乙商场一次摸出两个红球为事件![]() ,记盒子中
,记盒子中![]() 个白球为
个白球为![]() ,
, ![]() ,
, ![]() ,
, ![]() 个红球为
个红球为![]() ,
, ![]() ,
, ![]() ,记
,记![]() 为一次摸球的结果,则一切可能的结果有:
为一次摸球的结果,则一切可能的结果有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共
,共![]() 种.
种.
摸到的![]() 个球都是红球有
个球都是红球有![]() ,
, ![]() ,
, ![]() ,共
,共![]() 种.
种.
所以, ![]()
![]() .
.
因为![]() ,
,
所以,顾客在乙商场中奖的可能性大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为矩形,平面
为矩形,平面 平面
平面 ,
,  ,
,  ,
,  ,
,  为
为 中点.
中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)在棱
 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
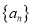 的前
的前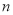 项和为
项和为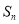 ,
,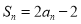 .
.(1)求数列
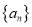 的通项公式;
的通项公式;(2)设
 ,
,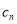 =
=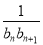 ,记数列
,记数列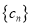 的前
的前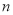 项和
项和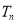 .若对
.若对 ,
, 恒成立,求实数
恒成立,求实数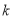 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①函数f(x)=( )x的递减区间是(﹣∞,+∞)
)x的递减区间是(﹣∞,+∞)
②已知函数f(x)的定义域为(0,1),则函数f(x+1)的定义域为(1,2);
③已知(x,y)映射f下的象是(x+y,x﹣y),那么(4,2)在f下的原象是(3,1).
其中正确命题的序号为 . -
科目: 来源: 题型:
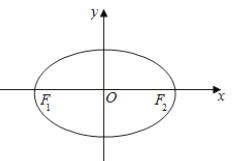
查看答案和解析>>【题目】已知
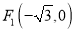 ,
, 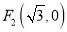 为椭圆
为椭圆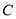 :
:  的左、右焦点,点
的左、右焦点,点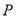 在椭圆
在椭圆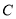 上,且
上,且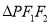 面积的最大值为
面积的最大值为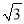 .
.
(Ⅰ)求椭圆
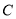 的方程;
的方程;(Ⅱ)若直线
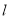 与椭圆
与椭圆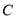 交于
交于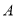 ,
, 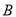 两点,
两点, 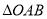 的面积为1,
的面积为1, 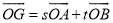 (
( ,
, 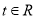 ),当点
),当点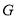 在椭圆
在椭圆 上运动时,试问
上运动时,试问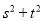 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出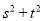 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中
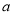 是0
是0 9的某个整数)
9的某个整数)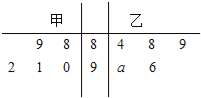
(1)若该厂决定从甲乙两人中选派一人去参加技能培训,从成绩稳定性角度考虑,你认为谁去比较合适?
(2)若从甲的成绩中任取两次成绩作进一步分析,在抽取的两次成绩中,求至少有一次成绩在(90,100]之间的概率.
相关试题

