【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() =
=![]() ,记数列
,记数列![]() 的前
的前![]() 项和
项和![]() .若对
.若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)关于项![]() 与
与![]() 的递推式,往往有两种解决方法,其一是转化为
的递推式,往往有两种解决方法,其一是转化为![]() 与
与![]() 的递推式,先求
的递推式,先求![]() 再求
再求![]() ;其二是转化为
;其二是转化为![]() 与
与![]() 的递推式再求
的递推式再求![]() ,其中
,其中![]() 是 转化桥梁,本题将已知条件转化为
是 转化桥梁,本题将已知条件转化为![]() ,得数列
,得数列![]() 为以2为公比的等比数列,进而求数列
为以2为公比的等比数列,进而求数列![]() 的通项公式;(2)首先求得
的通项公式;(2)首先求得![]() ,通过分析其结构,利用裂项相消法求和得
,通过分析其结构,利用裂项相消法求和得![]() ,带入
,带入![]() 中转化为恒成立问题求解.
中转化为恒成立问题求解.
试题解析:(1)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
即:![]() ,
,![]() 数列
数列![]() 为以2为公比的等比数列
为以2为公比的等比数列 ![]()
(2)由bn=log2an得bn=log22n=n,则cn=![]() =
=![]() =
=![]() -
-![]() ,
,
Tn=1-![]() +
+![]() -
-![]() + +
+ +![]() -
-![]() =1-
=1-![]() =
=![]() .
.
∵![]() ≤k(n+4),∴k≥
≤k(n+4),∴k≥![]() =
=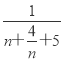 .
.
∵n+![]() +5≥2
+5≥2![]() +5=9,当且仅当n=
+5=9,当且仅当n=![]() ,即n=2时等号成立,
,即n=2时等号成立,
∴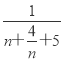 ≤
≤![]() ,因此k≥
,因此k≥![]() ,故实数k的取值范围为
,故实数k的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ﹣1
﹣1
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=|x|,g(x)=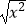
D.f(x)=1,g(x)=x0 -
科目: 来源: 题型:
查看答案和解析>>【题目】莫数学建模兴趣小组测量某移动信号塔
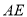 的高度
的高度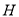 (单位:
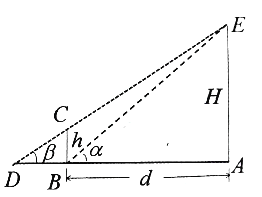
(单位: 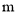 ),如图所示,垂直放置的标杆
),如图所示,垂直放置的标杆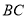 的高度
的高度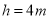 ,仰角
,仰角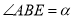 ,
, 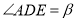 .
.
(Ⅰ)该小组已经测得一组
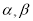 的值,
的值, 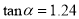 ,
, 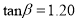 ,请推测
,请推测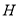 的值;
的值;(Ⅱ)该小组对测得的多组数据分析后,发现适当调节标杆到信号塔的距离
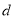 (单位:
(单位: 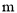 ),使得
),使得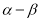 较大时,可以提高信号塔测量的精确度,若信号塔高度为
较大时,可以提高信号塔测量的精确度,若信号塔高度为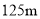 ,试问
,试问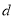 为多大时,
为多大时,  最大?
最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为矩形,平面
为矩形,平面 平面
平面 ,
,  ,
,  ,
,  ,
,  为
为 中点.
中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)在棱
 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中
①函数f(x)=( )x的递减区间是(﹣∞,+∞)
)x的递减区间是(﹣∞,+∞)
②已知函数f(x)的定义域为(0,1),则函数f(x+1)的定义域为(1,2);
③已知(x,y)映射f下的象是(x+y,x﹣y),那么(4,2)在f下的原象是(3,1).
其中正确命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计) 即为中奖.

乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.
问:购买该商品的顾客在哪家商场中奖的可能性大?
-
科目: 来源: 题型:
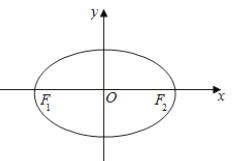
查看答案和解析>>【题目】已知
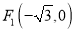 ,
, 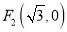 为椭圆
为椭圆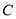 :
:  的左、右焦点,点
的左、右焦点,点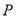 在椭圆
在椭圆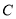 上,且
上,且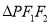 面积的最大值为
面积的最大值为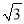 .
.
(Ⅰ)求椭圆
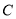 的方程;
的方程;(Ⅱ)若直线
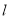 与椭圆
与椭圆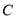 交于
交于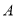 ,
, 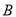 两点,
两点, 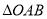 的面积为1,
的面积为1, 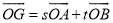 (
( ,
, 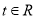 ),当点
),当点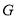 在椭圆
在椭圆 上运动时,试问
上运动时,试问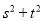 是否为定值?若是定值,求出这个定值;若不是定值,求出
是否为定值?若是定值,求出这个定值;若不是定值,求出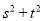 的取值范围.
的取值范围.
相关试题

