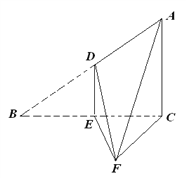
【题目】如图,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)可作![]() 于
于![]() ,利用所给条件,可证
,利用所给条件,可证![]() 为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明
为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明![]() ,可证得两平面垂直.
,可证得两平面垂直.
试题解析:(Ⅰ)D、E分别是AB、BC边的中点,![]() 平行且等于
平行且等于![]() 的一半,
的一半,![]() ,
,![]()
依题意,![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,∵
,∵![]() ,
,![]()
作![]() 于
于![]() ,则
,则![]() ,∵∠
,∵∠![]() ,
,![]()
梯形![]() 的面积
的面积![]()
四棱锥F-ADEC的体积![]()
(Ⅱ)(法一)取线段AF、CF的点N、Q,连接DN、NQ、EQ,则NQ平行且等于![]() 的一半,
的一半,![]() NQ平行且等于DE,DEQN是平行四边形,DN//EQ
NQ平行且等于DE,DEQN是平行四边形,DN//EQ
∵EC=EF,∠![]() ,
,![]() 是等边三角形,EQ
是等边三角形,EQ![]() ,又∵
,又∵![]() ,
,![]() ,
,![]() AC
AC![]() ,∵
,∵![]() ,
,![]()
![]() ,又
,又![]() ,
,![]()
(法二)连接BF,∵EC=EF,∠![]() ,
,![]() 是边长为2等边三角形
是边长为2等边三角形
∵BE=EF,![]() ,
,![]() ,
,![]()
![]() ,DE//AC,
,DE//AC,![]()
∵![]() ,
,![]() ,又∵
,又∵![]() ,,
,,![]()
又∵![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传3月5日学雷锋纪念日,重庆二外在高一,高二年级中举行学雷锋知识竞赛,每年级出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为
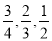 ,乙队每人答对的概率都是
,乙队每人答对的概率都是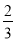 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用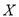 表示甲队总得分.
表示甲队总得分.(1)求随机变量
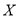 的分布列及其数学期望
的分布列及其数学期望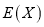 ;
;(2)求甲队和乙队得分之和为4的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
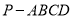 中,
中,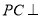 底面
底面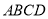 ,底面
,底面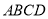 是直角梯形,
是直角梯形,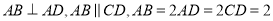 ,
,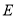 是
是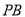 上的点.
上的点.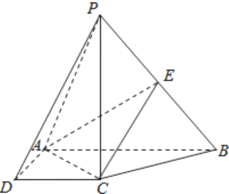
(1)求证: 平面
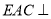 平面
平面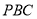 ;
; (2)若
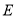 是
是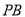 的中点,且二面角
的中点,且二面角 的余弦值为
的余弦值为 ,求直线
,求直线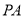 与平面
与平面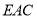 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
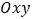 中,已知点
中,已知点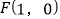 和直线
和直线 :
: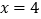 ,圆C与直线
,圆C与直线 相切,并且圆心C关于点
相切,并且圆心C关于点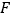 的对称点在圆C上,直线
的对称点在圆C上,直线 与
与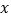 轴相交于点
轴相交于点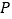 .
.(Ⅰ)求圆心C的轨迹E的方程;
(Ⅱ)过点
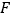 且与直线
且与直线 不垂直的直线
不垂直的直线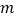 与圆心C的轨迹E相交于点A、B,求
与圆心C的轨迹E相交于点A、B,求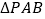 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差为0的等差数列{an}满足a1=1,且a1 , a3﹣2,a9成等比数列.
(1)求数列{an}的通项公式;
(2)记数列{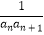 }的前n项和为Sn , 并求使得Sn>
}的前n项和为Sn , 并求使得Sn> 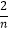 +
+  成立的最小正整数n.
成立的最小正整数n. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC中,
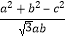 =
=  .
.
(1)求角A;
(2)若a=2,且sinB+cos(C+2B﹣ )取得最大值时,求△ABC的面积.
)取得最大值时,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字
 、
、 、
、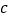 、
、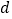 ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额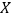 (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:方案


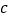
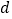
一
100
100
100
500
二
100
100
500
500
三
200
200
400
400
(Ⅰ)如果采取方案一,求
 的概率;
的概率;(Ⅱ)分别计算方案二、方案三的平均数
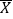 和方差
和方差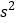 ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的
 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?方案二
方案三
合计
男性
12
女性
40
合计
82
100
附:
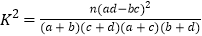
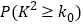
0.15
0.10
0.05
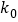
2.072
2.706
3.841
相关试题

