【题目】向量 ![]() =(1,2),
=(1,2), ![]() =(x,1),
=(x,1),
(1)当 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 平行时,求x;
平行时,求x;
(2)当 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直时,求x.
垂直时,求x.
参考答案:
【答案】
(1)解:∵向量 ![]() =(1,2),
=(1,2), ![]() =(x,1),
=(x,1),
∴ ![]() +2
+2 ![]() =(1,2)+2(x,1)=(2x+1,4)
=(1,2)+2(x,1)=(2x+1,4)
2 ![]() ﹣
﹣ ![]() =2(1,2)﹣(x,1)=(2﹣x,3).
=2(1,2)﹣(x,1)=(2﹣x,3).
当 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 平行时,则3(2x+1)﹣4(2﹣x)=0,解得x=
平行时,则3(2x+1)﹣4(2﹣x)=0,解得x= ![]()
(2)解:当 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直时,(2x+1)(2﹣x)+12=0,化为2x2﹣3x﹣14=0,解得x=﹣2或x=
垂直时,(2x+1)(2﹣x)+12=0,化为2x2﹣3x﹣14=0,解得x=﹣2或x= ![]() .
.
【解析】(1)利用向量共线定理即可得出.(2)利用向量垂直与数量积的关系即可得出.
【考点精析】掌握数量积判断两个平面向量的垂直关系是解答本题的根本,需要知道若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位有车牌尾号为
 的汽车
的汽车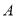 和尾号为
和尾号为 的汽车
的汽车 ,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,
,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,  车日出车频率
车日出车频率 ,
,  车日出车频率
车日出车频率 .该地区汽车限行规定如下:
.该地区汽车限行规定如下:车尾号
 和
和
 和
和
 和
和
 和
和
 和
和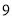
限行日
星期一
星期二
星期三
星期四
星期五
现将汽车日出车频率理解为日出车概率,且
 ,
,  两车出车相互独立.
两车出车相互独立.(I)求该单位在星期一恰好出车一台的概率.
(II)设
 表示该单位在星期一与星期二两天的出车台数之和,求
表示该单位在星期一与星期二两天的出车台数之和,求 的分布列及其数学期望
的分布列及其数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在无穷数列
 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
, . 设
. 设 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.(1)设数列
 为1,3,5,7,
为1,3,5,7, ,写出
,写出 ,
, ,
, 的值;
的值;(2)若
 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列 ;
;(3)设
 ,
, ,求
,求 的值.(用
的值.(用 表示)
表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)
 (x+1)2恒成立.
(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos2x﹣
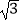 sinxcosx+1.
sinxcosx+1.
(1)求函数f(x)的单调递增区间;
(2)若f(θ)= ,θ∈(
,θ∈(  ,
, 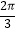 ),求sin2θ的值.
),求sin2θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(I)若
 ,求函数
,求函数 的单调区间.
的单调区间.(II)若函数
 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.(III)过坐标原点
 作曲线
作曲线 的切线,求切线的横坐标.
的切线,求切线的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,我们把使
,我们把使 的实数
的实数 叫做函数
叫做函数 的零点,且有如下零
的零点,且有如下零点存在定理:如果函数
 在区间
在区间 上的图像是连续不断的一条曲线,并且有
上的图像是连续不断的一条曲线,并且有 ,那么,函数
,那么,函数 在区间
在区间 内有零点.给出下列命题:
内有零点.给出下列命题:①若函数
 在
在 上是单调函数,则
上是单调函数,则 在
在 上有且仅有一个零点;
上有且仅有一个零点;②函数
 有
有 个零点;
个零点;③函数
 和
和 的图像的交点有且只有一个;
的图像的交点有且只有一个;④设函数
 对
对 都满足
都满足 ,且函数
,且函数 恰有
恰有 个不同的零点,则这6个零点的和为18;
个不同的零点,则这6个零点的和为18;其中所有正确命题的序号为________.(把所有正确命题的序号都填上)
相关试题

