【题目】设函数![]() .
.
(I)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(II)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
(III)过坐标原点![]() 作曲线
作曲线![]() 的切线,求切线的横坐标.
的切线,求切线的横坐标.
参考答案:
【答案】(1)减区间为![]() ,增区间为
,增区间为![]() .(2)
.(2)![]() (3)1
(3)1
【解析】试题分析:(1)求出![]() ,由
,由![]() 可得函数的减区间,由
可得函数的减区间,由![]() 可得函数的增区间;(2)转化成
可得函数的增区间;(2)转化成![]() 对任意
对任意![]() 恒成立求解,即
恒成立求解,即![]() 对任意
对任意![]() 恒成立,求出
恒成立,求出![]() 的最小值即可;(3)设出切点,结合导数的几何意义求出过切点的切线方程,利用切线过原点可求得切点坐标。
的最小值即可;(3)设出切点,结合导数的几何意义求出过切点的切线方程,利用切线过原点可求得切点坐标。
试题解析:(I)![]() 时,
时, ![]() ,
,
∴![]() .
.
∵当![]() ,
, ![]() ,
, ![]() 为单调减函数.
为单调减函数.
当![]() ,
, ![]() ,
, ![]() 为单调增函数.
为单调增函数.
∴![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(II)∵![]() ,
, ![]() 在区间
在区间![]() 上是减函数,
上是减函数,
∴![]() 对任意
对任意![]() 恒成立.
恒成立.
即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,
, ![]() .
.
易知![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() .
.
∴![]() .
.
(III)设切点为![]() ,
,
由题意得![]() ,
,
∴![]() ,
,
∴曲线在点切线方程为![]() ,
,
即![]() .
.
又切线过原点,
∴![]() ,
,
整理得![]() ,
,
设![]() ,
,
则![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
∴![]() 在
在![]() 上只有一个零点,即
上只有一个零点,即![]() ,
,
∴切点的横坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)
 (x+1)2恒成立.
(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】向量
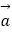 =(1,2),
=(1,2), 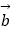 =(x,1),
=(x,1),
(1)当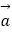 +2
+2 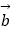 与2
与2 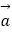 ﹣
﹣ 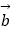 平行时,求x;
平行时,求x;
(2)当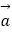 +2
+2 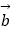 与2
与2 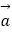 ﹣
﹣ 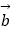 垂直时,求x.
垂直时,求x. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos2x﹣
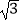 sinxcosx+1.
sinxcosx+1.
(1)求函数f(x)的单调递增区间;
(2)若f(θ)= ,θ∈(
,θ∈(  ,
, 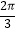 ),求sin2θ的值.
),求sin2θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,我们把使
,我们把使 的实数
的实数 叫做函数
叫做函数 的零点,且有如下零
的零点,且有如下零点存在定理:如果函数
 在区间
在区间 上的图像是连续不断的一条曲线,并且有
上的图像是连续不断的一条曲线,并且有 ,那么,函数
,那么,函数 在区间
在区间 内有零点.给出下列命题:
内有零点.给出下列命题:①若函数
 在
在 上是单调函数,则
上是单调函数,则 在
在 上有且仅有一个零点;
上有且仅有一个零点;②函数
 有
有 个零点;
个零点;③函数
 和
和 的图像的交点有且只有一个;
的图像的交点有且只有一个;④设函数
 对
对 都满足
都满足 ,且函数
,且函数 恰有
恰有 个不同的零点,则这6个零点的和为18;
个不同的零点,则这6个零点的和为18;其中所有正确命题的序号为________.(把所有正确命题的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l被两直线l1:4x+y+6=0和l2:3x﹣5y﹣6=0截得线段的中点为P(0,0),求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+blnx在x=1处有极值
 .
.
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
相关试题

